Частные производные функции многих переменных
Возьмем точку X = (х1, х2, …хn). Дадим аргументу х1 приращение Dх1, аргументу х2 приращение Dх2 и т.д., аргументу хn приращение Dхn; тогда функция z = f(x) получит приращение Dz = f(х1 + Dх1, х2 + Dх2, …хn + Dхn) - f(X). Эту величину называются полным приращением функции в точке X. Если задать приращение только одного из аргументов, то полученные приращения функции называю частными. Например, 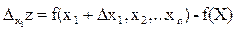 ,
, 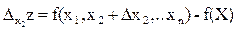 ,
, 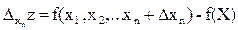 - частные приращения.
- частные приращения.
В общем случае полное приращение функции, не равно сумме частных, хотя иногда такая ситуация может иметь место.
Например, найдем частные и полное приращение функции
z = 1/(х1х2).
Частное приращение по аргументу х1 примет вид:
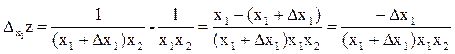
Частное приращение по аргументу х2 примет вид:
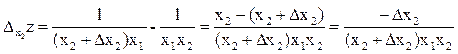
Полное приращение примет вид:
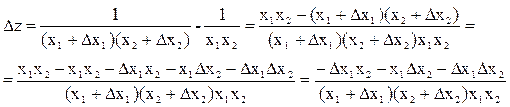
Можно показать, что в этом примере сумма частных приращений не равна полному приращению функции z:
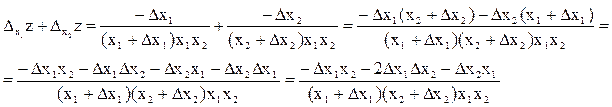
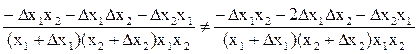
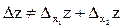
Частной производной функции нескольких переменных z = f (X) называют предел отношения соответствующего частного приращения функции к приращению рассматриваемого аргумента при стремлении последнего к нулю (если этот предел существует): 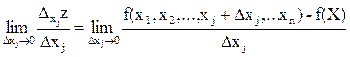 .
.
Частную производную обозначают 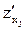 или ¶z/¶xj.
или ¶z/¶xj.
Из определения частных производных следует, что для нахождения производной ¶z/¶xj надо считать постоянными все переменные аргументы, кроме одного - xj.
В частности, если z представляет собой функцию двух переменных x и y (z = f(x,y)), то ее частная производная по х равна 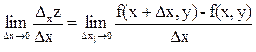 , и для ее нахождения надо считать постоянным аргумент y. Частная производная z по y равна
, и для ее нахождения надо считать постоянным аргумент y. Частная производная z по y равна 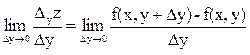 , и для ее нахождения надо считать постоянным аргумент х.
, и для ее нахождения надо считать постоянным аргумент х.
Например, найдем частные производные следующих функций:
Пример 1. z = x ln y + y/x
Чтобы найти частную производную по х, считаем у постоянной величиной. Тогда , zx' = ln y * (x)' + y*(1/x)' = ln y + y*(-1)*x-2 = ln y – y/(x2).
Аналогично продифференцируем эту функцию по у, считаея х постоянной: zy' = x (ln y)' + (1/x)*(y)' = x/y + 1/x
Пример 2. z = xy
Частная производная по х представляет собой производную степенной функции, т.е. zx' = yxy-1.
Частная производная по y представляет собой производную показательной функции, т.е. zy' = xyln x.
Понятие частной производной имеет вполне четкий экономический смысл. Поскольку функции нескольких переменных в экономике выражают зависимость некоторой величины от нескольких других факторов (иногда включая время), частная производная выступает как скорость изменения этой величины во времени или относительного другого исследуемого фактора при условии, что остальные факторы не меняются.
Например, пусть магазин продает мороженое – сливочное по 25 руб. за штуку, шоколадное по 30 руб. за штуку и фисташковое по 32 руб. за штуку. Обозначим х1 – объем продаж сливочного мороженого (шт.), х2 – объем продаж шоколадного мороженого (шт.), х3 – объем продаж фисташкового мороженого (шт.). Тогда выручку z (руб.) магазина от продажи этих сортов мороженого можно рассчитать с помощью функции трех переменных z = 25х1 + 30х2 + 32х3. Найдем частную производную этой функции по х1: 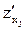 = 25. Каков экономический смысл этой величины? Она показывает, на сколько возрастет выручка при единичном изменении продаж сливочного мороженого, при условии, что продажи остальных видов мороженого останутся на прежнем уровне. Иными словами, это скорость изменения общей выручки относительно изменения продаж сливочного мороженого. Аналогичные рассуждения можно провести для обеих других переменных.
= 25. Каков экономический смысл этой величины? Она показывает, на сколько возрастет выручка при единичном изменении продаж сливочного мороженого, при условии, что продажи остальных видов мороженого останутся на прежнем уровне. Иными словами, это скорость изменения общей выручки относительно изменения продаж сливочного мороженого. Аналогичные рассуждения можно провести для обеих других переменных.
Рассмотренное выше понятие частной производной относится к частной производной первого порядка. Введем понятия частных производных более высоких порядков.
Если частные производные первого порядка являются дифференцируемыми функциями, то можно найти и их частные производные, которые называются частными производными второго порядка: 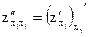 . На основании частных производных второго порядка можно вычислить частные производные третьего порядка и т.д.
. На основании частных производных второго порядка можно вычислить частные производные третьего порядка и т.д.
Можно доказать, что если частные производные второго порядка функции z = f(x, у) непрерывны в некоторой точке, то в этой точке 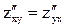 .
.
Дата добавления: 2015-10-06; просмотров: 1092;
