ПОЛЕ ЭЛЕКТРИЧЕСКОГО ДИПОЛЯ
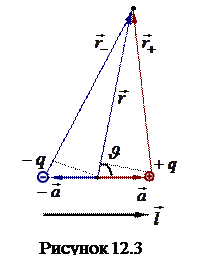 Электрическим диполем называется система двух одинаковых по величине, но противоположных по знаку зарядов, расстояниеl между которыми намного меньше расстояния до точек, в которых определяется его поле. Осью диполя называется прямая, проходящая через заряды диполя. На примере поля диполя покажем, как можно использовать вычисление потенциала для нахождения напряженности поля.
Электрическим диполем называется система двух одинаковых по величине, но противоположных по знаку зарядов, расстояниеl между которыми намного меньше расстояния до точек, в которых определяется его поле. Осью диполя называется прямая, проходящая через заряды диполя. На примере поля диполя покажем, как можно использовать вычисление потенциала для нахождения напряженности поля.
Очевидно, что поле диполя обладает осевой симметрией. Это означает, что в любой плоскости, проходящей через ось диполя, картина силовых линий поля одинакова.
Положение точек будем характеризовать радиус-вектором 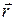 , проведенным из центра диполя или полярными координатами
, проведенным из центра диполя или полярными координатами 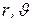 . Пусть положительный заряд имеет радиус-вектор
. Пусть положительный заряд имеет радиус-вектор 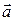 , отрицательный
, отрицательный 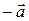 . По определению диполя
. По определению диполя 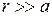 . Тогда приближенно можно считать, что расстояния от зарядов рассматриваемой точки равны
. Тогда приближенно можно считать, что расстояния от зарядов рассматриваемой точки равны
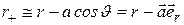 (12.28)
(12.28)
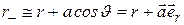 (12.29)
(12.29)
Тогда потенциал рассматриваемой точки
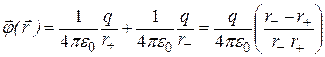 (12.30)
(12.30)
Учтем, что в силу того, что 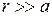 , можно использовать приближенные соотношения:
, можно использовать приближенные соотношения:
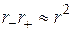 ;
; 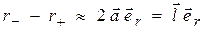 , (12.31)
, (12.31)
где 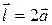 .
.
Тогда
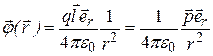 (12.32)
(12.32)
где 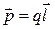 по определению называют электрическим моментом диполя.
по определению называют электрическим моментом диполя.
В полярных координатах 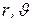 выражение для потенциала будет иметь вид:
выражение для потенциала будет иметь вид:
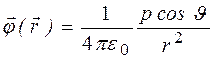 (12.33)
(12.33)
Для того чтобы получить выражение для напряженности поля, найдем проекции 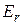 и
и 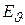 вектора
вектора 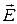 на два взаимно перпендикулярных направления: одно из них определяется движением точки, вызванным изменением
на два взаимно перпендикулярных направления: одно из них определяется движением точки, вызванным изменением 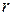 при фиксированном
при фиксированном 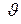 , другое - изменением
, другое - изменением 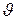 при фиксированном
при фиксированном 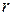 . Проекция
. Проекция
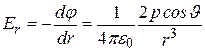 (12.34)
(12.34)
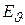 найдем как отношение
найдем как отношение 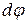 к приращению расстояния, приходящему при изменении
к приращению расстояния, приходящему при изменении 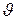 на
на 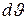 : это расстояние равно
: это расстояние равно 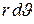 :
:
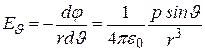 (12.35)
(12.35)
Тогда квадрат модуля
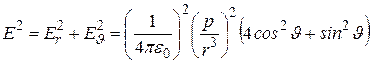 . (12.36)
. (12.36)
Квадратный корень из (12.36) дает модуль вектора напряженности:
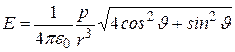 . (12.37)
. (12.37)
Рассмотрим структуру поля диполя. Для этого найдем напряженность поля на оси диполя  и на прямой, перпендикулярной оси диполя и проходящий через его центр
и на прямой, перпендикулярной оси диполя и проходящий через его центр  и построим примерный вид силовых линий поля диполя.
и построим примерный вид силовых линий поля диполя.
 На оси диполя
На оси диполя 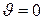 или
или 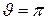 , и проекция
, и проекция 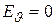 , поскольку
, поскольку 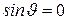 . Проекция составляющей
. Проекция составляющей 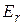 (на направление возрастания r) имеет противоположные знаки с двух сторон от диполя:
(на направление возрастания r) имеет противоположные знаки с двух сторон от диполя:
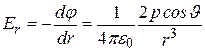 , т.е.
, т.е. 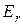 > 0 для
> 0 для 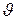 = 0 (справа от диполя) и
= 0 (справа от диполя) и 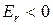 для
для 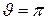 (слева от диполя). Следовательно, вектор
(слева от диполя). Следовательно, вектор 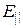 совпадет по направлению с электрическим моментом
совпадет по направлению с электрическим моментом 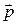 диполя и справедливо векторное равенство:
диполя и справедливо векторное равенство:
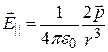 (12.38)
(12.38)
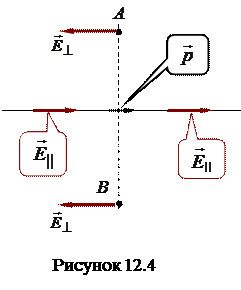 На прямой, перпендикулярной оси диполя и проходящей через его центр
На прямой, перпендикулярной оси диполя и проходящей через его центр 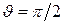 . Поэтому
. Поэтому 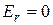 , и напряженность определяется
, и напряженность определяется 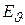 :
:
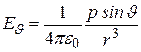
В точке  возрастанию
возрастанию  соответствует направление навстречу электрическому моменту диполя, поэтому вектор
соответствует направление навстречу электрическому моменту диполя, поэтому вектор 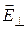 совпадает по знаку с
совпадает по знаку с 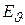 и направлен противоположно электрическому моменту диполя
и направлен противоположно электрическому моменту диполя 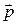 .
.
В точке 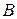 возрастанию
возрастанию 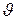 соответствует направление вдоль электрического момента диполя, но
соответствует направление вдоль электрического момента диполя, но 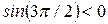 , и
, и 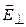 оказывается направленным противоположно электрическому моменту диполя
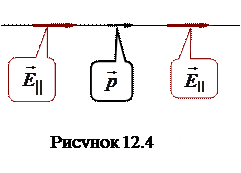
оказывается направленным противоположно электрическому моменту диполя 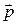 . Поэтому картину силовых линий диполя можно изобразить приблизительно так, как это показано на рисунке 12.5.
. Поэтому картину силовых линий диполя можно изобразить приблизительно так, как это показано на рисунке 12.5.
Второй важной особенностью поля диполя является тот факт, что модуль вектора напряженности убывает пропорционально 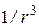 . Быстрое убывание модуля вектора напряженности поля является характерной особенностью полей, создаваемых нейтральными в целом системами зарядов.
. Быстрое убывание модуля вектора напряженности поля является характерной особенностью полей, создаваемых нейтральными в целом системами зарядов. 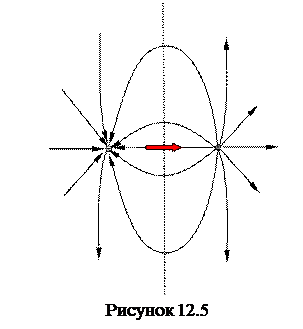 Так для системы четырех зарядов квадруполь) напряженность создаваемого поля оказывается пропорциональным
Так для системы четырех зарядов квадруполь) напряженность создаваемого поля оказывается пропорциональным 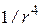 , а поле системы восьми зарядов (октуполь) убывает как
, а поле системы восьми зарядов (октуполь) убывает как 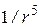 .
.
Наконец, необходимо отметить, что взаимодействие электрических моментов молекул является важной составляющей взаимодействия молекул, приводящего к существованию их ван-дер-ваальсовского притяжения на больших расстояниях.
Дата добавления: 2015-09-14; просмотров: 2646;
