СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ПОЛЯ И ПОТЕНЦИАЛОМ
Одно и тоже электрическое поле можно охарактеризовать напряженностью и потенциалом. Естественно между этими характеристиками должна существовать связь, и ее легко установить. Как мы знаем, по определению 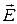 ~
~ 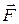 , а
, а 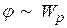 , и между ними существует связь:
, и между ними существует связь:
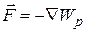 (12.21)
(12.21)
Разделив (12.21) на величину пробного заряда получим соотношение, связывающее напряженность поля в данной точке пространства и потенциал этой точки:
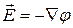 . (12.22)
. (12.22)
Напомним, что в соответствии с определением градиента
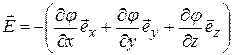 . (12.23)
. (12.23)
В соответствии с соотношением(12.23) если в пространстве некоторой осью 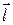 задано направление, то проекция
задано направление, то проекция 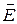 на это направление может быть найдена по формуле:
на это направление может быть найдена по формуле:
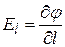 (12.24)
(12.24)
Часто бывает необходимо решить обратную задачу: по известному распределению в пространстве 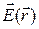 найти разность потенциалов между двумя точками. В этом случае можно рассуждать так. Работа поля при перемещении заряда из точки 1 в точку 2 определяется соотношением:
найти разность потенциалов между двумя точками. В этом случае можно рассуждать так. Работа поля при перемещении заряда из точки 1 в точку 2 определяется соотношением:
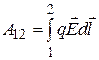 (12.25)
(12.25)
С другой стороны эту же работу можно найти по формуле
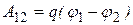 (12.26)
(12.26)
А значит:
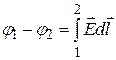 (12.27)
(12.27)
 При рассмотрении электростатических задач часто используют понятие эквипотенциальной поверхности. Как следует из названия, такой поверхностью называют поверхность, все точки которой имеют одинаковый потенциал. Важным свойством эквипотенциальной поверхности является то, что в каждой точке она перпендикулярна силовым линиям поля (линиям вектора
При рассмотрении электростатических задач часто используют понятие эквипотенциальной поверхности. Как следует из названия, такой поверхностью называют поверхность, все точки которой имеют одинаковый потенциал. Важным свойством эквипотенциальной поверхности является то, что в каждой точке она перпендикулярна силовым линиям поля (линиям вектора 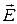 ). Действительно, если бы это было не так (т.е. если бы в данной точке эквипотенциальной поверхности вектор напряженности не был бы ей перпендикулярен и имел бы ненулевую тангенциальную составляющую вдоль некоторого направления), то при перемещении на dl вдоль этого направления потенциал должен был бы получать ненулевое приращение
). Действительно, если бы это было не так (т.е. если бы в данной точке эквипотенциальной поверхности вектор напряженности не был бы ей перпендикулярен и имел бы ненулевую тангенциальную составляющую вдоль некоторого направления), то при перемещении на dl вдоль этого направления потенциал должен был бы получать ненулевое приращение 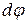 . Это следует из соотношения (12.24)
. Это следует из соотношения (12.24) 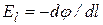 . Но тогда поверхность вдоль этого направления не должна быть эквипотенциальной! Поскольку по условию при перемещении по эквипотенциальной поверхности на dl изменение потенциала
. Но тогда поверхность вдоль этого направления не должна быть эквипотенциальной! Поскольку по условию при перемещении по эквипотенциальной поверхности на dl изменение потенциала 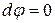 , тангенциальная составляющая
, тангенциальная составляющая 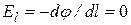 , и вектор
, и вектор 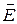 перпендикулярен эквипотенциальной поверхности.
перпендикулярен эквипотенциальной поверхности.
Если потенциальные поверхности проводить так, чтобы разность потенциалов между соседними поверхностями оставалась постоянной, то по густоте эквипотенциальных поверхностей можно судить о величине напряженности электрического поля, как это показано на рисунке 12.3 для точечного положительного заряда.
Дата добавления: 2015-09-14; просмотров: 710;
