НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

На правах рукописи

Физика

Конспект лекций

(Часть 3. Электростатика и постоянный ток)

Для студентов направления 230400

«Информационные системы и технологии»

Электронный образовательный ресурс

Составитель: к.ф.-м.н., доцент В.В. Коноваленко

Рассмотрен и рекомендован для использования в учебном процессе на 2013/2014 – 2015/2016 уч. г. на заседании кафедры ЕНД.

Протокол № 1 от 04. 09. 2013 г.

Шахты 2013

НАПРЯЖЕННОСТЬ И ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.

ЭЛЕКТРИЧЕСКИЙ ДИПОЛЬ

ЭЛЕКТРИЧЕСКИЙ ЗАРЯД.

Электрические заряды. Дискретность заряда. Элементарный заряд. Закон сохранения электрического заряда. Единица заряда. Точечный заряд. Закон Кулона. Системы единиц измерений.

Самостоятельно.

НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

Всякий электрический заряд изменяет свойства окружающего его пространства таким образом, что на другие электрические заряды он воздействует с некоторой силой. Другими словами всякий заряд создает вокруг себя поле. Если взаимодействующие заряды покоятся, то взаимодействие между ними осуществляется посредством электростатического поля. По величине силы, действующей на некоторый данный заряд (пробный), можно судить о «силе» или «интенсивности» поля. Для характеристики поля в точке необходимо, чтобы пробный заряд был точечным. По определению напряженностью электрического поля называется векторная величина, равная отношению силы 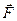, действующей на точечный пробный заряд в данной точке поля, к величине этого заряда q:

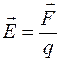(12.1).

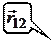
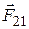Как известно, точечные заряды взаимодействуют по закону Кулона, согласно которому сила , действующая на заряд 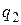со стороны заряда 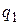(рисунок 12.1):

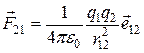, (12.2)

где 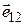- орт радиус-вектора 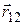, проведенного от 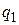к .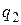

Соответственно напряженность поля точечного заряда в точке с радиус-вектором 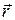, проведенным от заряда в данную точку, описывается формулой:

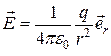(12.3)

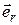- орт радиус-вектора .

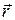Для наглядного изображения электрического поля используют линии вектора 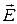или силовые линии электрического поля. По определению, эти линии проводят так, чтобы

► касательная к силовой линии в данной точке давала бы направление вектора напряженности 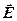в данной точке;

► густота линий, т.е. количество линий, пронизывающих единичную площадку поверхности, перпендикулярной силовым линиям, была бы равна модулю вектора ;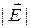

► линии направлены от положительного заряда к отрицательному.

Очевидно, что описание поля с помощью изображения силовых линий является условным и очень приближенным, тем не менее наглядность такого представления о поле оказывается очень полезной.

Поле точечного заряда является центральным, поскольку соответствует обоим признакам центральности поля: сила в любой точке пространства проходит через центр (точку, в которой находится заряд, создающий поле) и по модулю зависит только от расстояния до этого заряда. Силовые линии поля положительного и отрицательного зарядов показаны на рисунке 12.2.

Линии напряженности электрического поля начинаются и заканчиваются только на зарядах, либо уходят в бесконечность. Действительно, рассмотрим поле точечного заряда (Произвольный заряд всегда образован точечными). Число линий, пересекающих произвольную сферу радиуса r, в центре которой находится заряд, равно произведению модуля вектора напряженности, т.е. густоты линий, на площадь сферы: 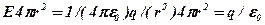, т.е. не зависит от радиуса окружности. А значит, на любом расстоянии от q число линий будет одинаковым. Очевидно, что этот вывод можно распространить на любые заряды

Экспериментально установлено, что сила, действующая на данный заряд со стороны системы зарядов, равна векторной сумме сил, действующих со стороны каждого из зарядов системы. Вследствие этого для напряженности поля системы зарядов можно записать формулу:

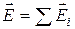, (12.4)

где 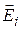- напряженность поля, создаваемая i-тым зарядом системы. Это утверждение называется принципом суперпозиции полей. Смысл и важность этого утверждения заключается в том, что на его основе можно, в принципе, вычислить поле произвольной системы зарядов, разбив ее мысленно на достаточно малые порции dq, которые можно считать точечными зарядами.