ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
Рассмотрим поле точечного заряда. Поскольку оно является центральным, то, как всякое центральное, потенциальным. Следовательно, работа сил электростатическогополя поля не зависит от формы пути. По закону Кулона сила, действующая на заряд 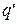 в поле заряда
в поле заряда 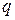 ,
,
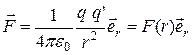 (12.5)
(12.5)
Работа сил поля заряда q при перемещении 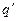 из точки 1 в 2.
из точки 1 в 2.
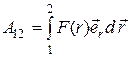 (12.6)
(12.6)
Учтем, что скалярное произведение приращения вектора 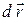 на орт этого вектора
на орт этого вектора 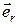 равно приращению модуля вектора:
равно приращению модуля вектора: 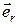
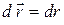 . Тогда
. Тогда
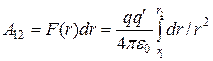 (12.7)
(12.7)
Интегрируя, получаем:
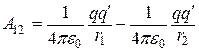 (12.8)
(12.8)
С другой стороны, работа консервативных сил может быть представлена как убыль потенциальной энергии:
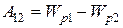 (12.9)
(12.9)
Сравнивая (12.8) и (12.9), приходим к выводу, что потенциальная энергия заряда 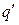 в поле точечного заряда
в поле точечного заряда 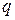 выражается формулой:
выражается формулой:
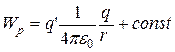 (12.10)
(12.10)
Значение константы в (12.10) выбирают так, чтобы на бесконечности потенциальная энергия обращалась в нуль. Следовательно, потенциальная энергия 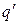 в поле, созданном q определяется выражением:
в поле, созданном q определяется выражением:
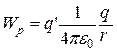 (12.11)
(12.11)
У различных зарядов 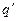 в данной точке поля будет, очевидно, различная потенциальная энергия. Однако ее отношение к
в данной точке поля будет, очевидно, различная потенциальная энергия. Однако ее отношение к 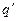 будет оставаться постоянным и может использоваться как характеристика поля в данной точке. Поэтому по определению потенциалом
будет оставаться постоянным и может использоваться как характеристика поля в данной точке. Поэтому по определению потенциалом 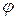 поля в данной точке называется скалярная величина.
поля в данной точке называется скалярная величина.
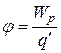 (12.12)
(12.12)
В соответствии с этим определением потенциал точки в поле, созданном точечным зарядом, выражается соотношением:
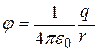 (12.13)
(12.13)
Если поле создано системой N точечных зарядов, то работа 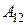 , совершаемая полями каждого из зарядов системы при перемещении заряда
, совершаемая полями каждого из зарядов системы при перемещении заряда 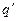 из точки 1 в точку 2 равна алгебраической сумме работ
из точки 1 в точку 2 равна алгебраической сумме работ 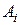 , совершаемых полем каждого из зарядов системы:
, совершаемых полем каждого из зарядов системы:
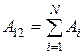 , (12.14)
, (12.14)
а потенциальная энергия алгебраической сумме  Соответственно, потенциал поля системы зарядов равен алгебраической сумме потенциалов каждого из зарядов системы:
Соответственно, потенциал поля системы зарядов равен алгебраической сумме потенциалов каждого из зарядов системы:
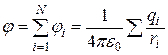 (12.15)
(12.15)
Формула (12.15) поясняет смысл введения в рассмотрение потенциала, как характеристики электрического поля. При вычислении потенциала системы зарядов достаточно алгебраически сложить потенциалы зарядов системы. Если же использовать для характеристики поля его напряженность, то необходимо осуществлять векторное сложение, что почти всегда оказывается намного сложнее.
По определению потенциала, заряд q в точке с потенциалом 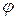 обладает потенциальной энергией
обладает потенциальной энергией
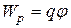 (12.15)
(12.15)
Следовательно, работа сил поля при перемещении заряда из точки 1 в 2 может быть найдена по формуле:
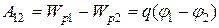 (12.16)
(12.16)
5 В частном случае, если заряд удаляется на бесконечность, где значение потенциала принято равным нулю 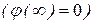 , силы поля совершают работу:
, силы поля совершают работу:
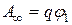 . (12.17)
. (12.17)
Формула (12.17) позволяет сформулировать физический смысл понятия потенциала: потенциал численно равен работе, совершаемой силами поля над единичным положительным зарядом при его перемещении из данной точки поля на бесконечность.
Дата добавления: 2015-09-14; просмотров: 588;
