Градиент, оператор Гамильтона

Далее мы рассмотрим некоторые дифференциальные операции с векторыми и скалярными полями, а именно градиент, дивергенцию (расхождение) и ротор (вихрь). Эти операции потребуются нам при рассмотрении уравнений Максвелла.

Каждое поле порождает собой еще три поля, которые мы и будем рассматривать: векторные поля градиента и ротора и скалярное поле дивергенции.

Градиентом скалярного поля 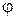называется вектор, имеющий направление быстрейшего увеличения 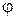и по величине равный производной по этому направлению.

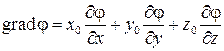
В векторном анализе часто удобно использовать условный вектор, т.н. оператор Гамильтона. В декартовых координатах он имеет вид

.

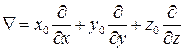Тогда можно записать

.

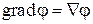Градиент совпадает по направлению с нормалью к поверхности уровня 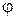и направлен в ту сторону, куда 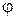возрастает (рисунок 13).

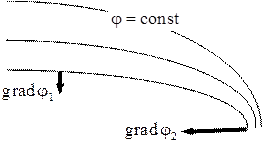
Рисунок 13 − Градиент

Градиент будет применяться при анализе потенциальных векторных полей. Другое применение вектора градиента – численная оптимизация функций.