Скалярные и векторные поля. Изображение полей. Примеры скалярных и векторных полей

До сих пор мы рассматривали отдельные векторы или скаляры. Рассмотрим более сложный случай, когда с каждой точкой пространства связывается значение некоторого скаляра или вектора. Рассматриваемая часть пространства называется тогда полем, скалярным или векторным.

Так, например, в атмосфере мы имеем скалярное поле давления, т.к. каждой точке атмосферы отвечает некоторое значение давления. В реке мы имеем векторное поле скорости; вокруг передающей радиоантенны – векторное электромагнитное поле.

Аналитически задание скалярной функции 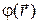сводится к заданию функции 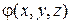от трех координат точки, задание векторной функции 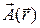равносильно заданию трех скалярных функций 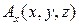, , 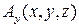, дающих компоненты вектора .

Очень часто приходится рассматривать скалярные или векторные функции, изменяющиеся с течением времени: , 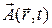. Соответствующие им поля называются тогда переменными или нестационарными.

Для наглядности большое значение имеет графическое представление полей. Проще всего обстоит дело с двумерными скалярными полями: они изображаются в виде карт, контурных диаграмм, поверхностей и т.п. Примеры таких изображений приведены на рисунке 6; следует иметь в виду, что здесь изображено «плоское» скалярное поле двух координат , для поля трех координат приходится строить семейство поверхностей или карт.

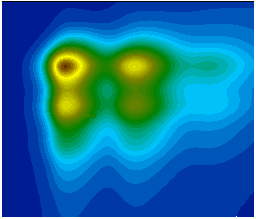
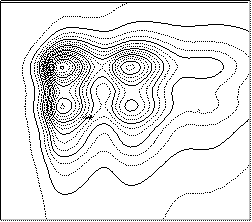
карта контурная диаграмма

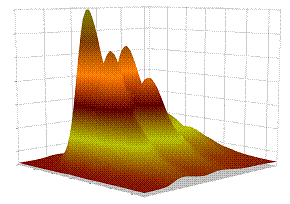
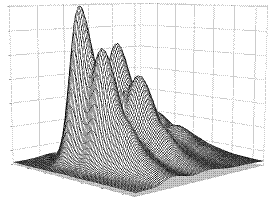
цветная поверхность сетчатая поверхность

Рисунок 6 − Изображение скалярных полей

Рассмотрим теперь векторное поле. Наиболее просто нанести на поле равномерную сетку и в каждом узле сетки изобразить вектор обычным образом, т.е. в виде направленного отрезка (рисунок 7).

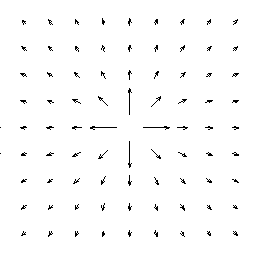
Рисунок 7 − Изображение векторного поля векторами на сетке

Однако для более наглядного изображения векторного поля удобно использовать векторные линии, предложенные Фарадеем, т.е., такие линии, во всякой точке которых вектор будет иметь направление касательное к линии (рисунок 8).

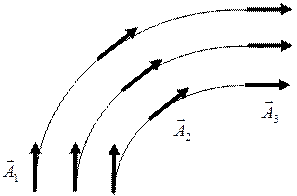
Рисунок 8 − Построение векторных линий

Приближенно мы можем построить эти линии следующим образом. Выберем какую-нибудь точку поля и отложим вдоль отвечающего этой точке вектора отрезок малой длины. В конце этого отрезка поступим аналогично, и будем продолжать так дальше. В результате будет получена ломаная линия, которая тем ближе будет представлять нашу векторную линию, чем короче отрезки берутся.

Однако задание векторных линий и их ориентировка дает нам только направление вектора во всякой точке поля, величину же вектора мы должны графически изобразить каким-либо другим способом. Обычно величина вектора характеризуется густотой проводимых линий, как показано на рисунке 9.

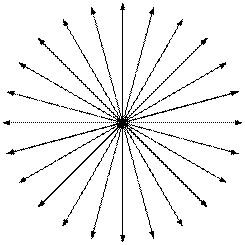
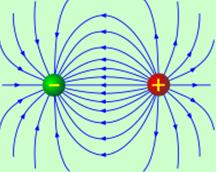
Рисунок 9 − Векторные линии