Циркуляция вектора и поток вектора через поверхность

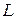Пусть нам задано векторное поле вектора ; возьмем какую-нибудь кривую , соединяющую две точк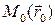и и 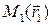, разобьем ее на бесконечно малые элементы, которые заменим хордами 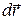, составим далее скалярные произведения 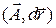, где есть вектор поля, отвечающий началу вектора 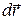. Составим далее сумму всех таких скалярных произведений и перейдем к пределу, устремив все элементы 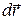к нулю. Полученный предел называется линейным интегралом вектора вдоль кривой 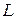и обозначается через

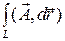
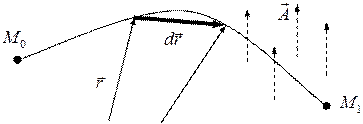
Рисунок 10 − К определению линейного интеграла вектора

Линейный интеграл вычисляется через интегрирование проекций вектора на оси координат:

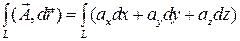
Если кривая 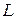замкнута, то линейный интеграл вектора называется циркуляцией вектора по этой кривой. К знаку интеграла в этом случае добавляется кружок: .

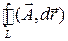С помощью векторов можно изображать не только направленные отрезки, но и направленные площади. Для этого вернемся к определению векторного произведения: там нам тоже встретилась площадь в виде параллелограмма, построенного на векторах и 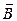, причем был важен порядок, в котором следовали вектора. Откладывая сначала вектор , а затем 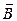, получим определенное направление контура параллелограмма.

Представление площадей векторами необходимо для введения понятия потока вектора через поверхность. Поток вектора через поверхность является поверхностным интегралом вектора по поверхности 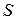. Определим его следующим образом. В каждой точке поверхности проведем единичный вектор нормали 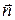. Если − значение вектора в некоторой точке M поверхности S, то проекция на единичный 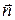определяется через скалярное произведение (рисунок 11):

.

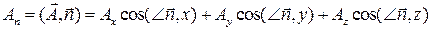Рисунок 11 − К определению потока вектора через поверхность

Разделим теперь поверхность S на большое число малых элементов, каждый из них изображается, как мы определили выше, вектором 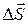. Размерность будет выражаться в единицах измерения площади – м²_. Например, если мы впишем в поверхность S многогранную поверхность, то каждая ее грань будет изображаться вектором, направленным по нормали к этой грани и равным по величине площади грани. Составим для каждого элемента скалярное произведение 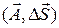и образуем сумму 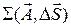, распространенную по всем элементам поверхности. Эта сумма стремится к пределу, когда все элементы поверхности стремятся к нулю. Получаемый предел обозначается как

,

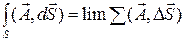и называется поверхностным интегралом вектора по поверхности S или потоком вектора через поверхность S. Вычисление потока выполняется следующим образом:

.

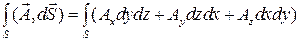Поток вектора положителен, если силовые линии выходят из поверхности S наружу, и отрицателен, если они входят внутрь – потому что угол между и 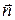в первом случае острый, и косинус больше нуля, а во втором – тупой.

Если поверхность 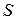замкнутая, то к знаку интеграла добавляется кружок: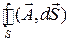

Понятие потока вектора появилось в гидродинамике, которая развилась раньше теории электричества. Если через 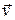обозначить вектор скорости течения жидкости, то выражение

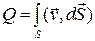
будет представлять собой количество жидкости, проходящее через эту поверхность в единицу времени, т.е., действительно поток. Следует отметить, что в применении к векторам электромагнитного поля слово «поток» имеет только математическое значение, подчеркивающее сходство формул, но никак не сходство физических явлений.