Дивергенция, физический смысл дивергенции

Для анализа явлений, происходящих в электромагнитном поле, важно знать, где находятся источники того или иного вектора. За меру источника можно выбрать поток вектора через замкнутую поверхность, но внутри данной замкнутой поверхности могут быть источники разных знаков, взаимно уничтожающие свое действие. Чтобы выявить распределение источников в пространстве, можно устремить эту замкнутую поверхность к нулю, но тогда поток вектора через эту бесконечно малую поверхность будет бесконечно малым. Это затруднение ликвидируется тем, что поток вектора через замкнутую поверхность делят на объем, окруженный этой поверхностью. Устремляя объем к нулю, получим предел этого отношения, который и называется дивергенцией.

Дивергенция дает возможность точно указать, в каких точках пространства расположились источники вектора.

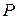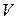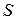Возьмем какую-либо точку поля , окружим ее малым объемом и вычислим поток вектора через поверхность , ограничивающую объем 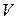. Разделим этот поток на 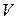, чтобы отнести его к единице объема и перейдем к пределу, устремляя к нулю все размеры 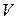, что мы будем обозначать символом 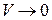. При этом объем 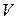будет стягиваться к точке 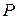. В результате получится некоторое число, зависящее от поведения вблизи точки 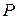, и характеризующее степень истечения из точки 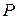. Это число называется расхождением, или дивергенцией вектора в точке . 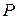Дивергенция обозначается символом 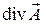. Таким образом,

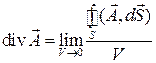
В векторном анализе доказывается, что

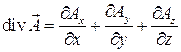
или, с применением оператора Гамильтона,

,

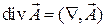т.е., скалярное произведение оператора набла на вектор .

Рассмотрим значения дивергенции для разных случаев поля (рисунок 14).

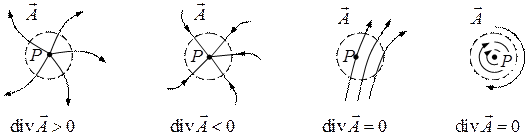
Рисунок 14 − Дивергенция

При положительной в точке 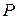дивергенции внутри области 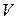поток вектора через ограничивающую поверхность больше нуля, то есть линии вектора расходятся из этой области. Таким образом, внутри 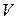находятся источники вектора . При отрицательной дивергенции, наоборот, линии вектора сходятся в область 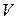и тогда внутри нее находятся стоки векторного поля.

Если же во всех точках некоторой области поля дивергенция оказывается равной нулю, что силовые линии поля либо пронизывают ее, либо являются замкнутыми.