Теорема Стокса

Из определения проекции ротора на направление нормали 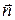вытекает теорема Стокса, имеющая важное значение при выводе уравнений Максвелла. Теорема Стокса относится к контуру произвольных размеров и опирающейся на него поверхности. Для вывода выражения, представляющего собой теорему Стокса, разобьем поверхность 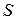, опирающуюся на контур 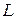, на большое число малых поверхностей 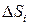, каждая из которых ограничена малым контуром 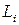(рисунок 16). Для каждой из малых поверхностей, составляющих вместе большую, будет приближенно справедливо выражение для проекции ротора на нормаль к поверхности, которое можно переписать в виде

,

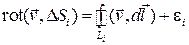где 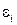− малая величина более высокого порядка малости, чем 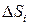. Здесь 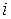− номер контура и соответствующего элемента поверхности, так что равенства подобного вида будут записаны для всех элементов.

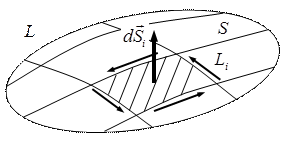
Рисунок 16 − Теорема Стокса

Сложим теперь эти равенства для всех элементов, в результате чего получим:

.

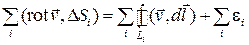Рассмотрим сумму циркуляций в правой части этого уравнения. Все контуры 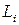должны иметь одинаковое направление обхода, так как нормали к элементам поверхности направлены в одну сторону, а направление нормали и обхода связаны между собой правилом правого винта. Поэтому соседние линии двух контуров, соприкасающихся между собой, будут направлены в противоположные стороны, и так будет для любой пары соседних линий. Следовательно, циркуляции по всем этим соседним участкам будут иметь одинаковую величину и противоположные знаки, и при сложении всех циркуляций останется только циркуляция по внешнему контуру, так как для внешнего контура не будет парных ему участков контура, направленных в противоположную сторону. Вследствие этого, для любого разбиения поверхности на участки, получится равенство

.

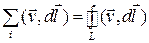Это равенство будет справедливо и тогда, когда поверхность разбита на небольшое количество участков, так как оно основано на взаимном уничтожении циркуляций на линиях раздела соседних участков, в результате чего остается только циркуляция по внешнему контуру.

Будем увеличивать число площадок на поверхности до бесконечности при одновременном уменьшении их размеров. В пределе сумма в левой части перейдет в интеграл, а последнее слагаемое в правой части исчезнет и все равенство примет следующий вид:

.

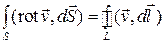Это равенство дает содержание теоремы Стокса: поверхностный интеграл ротора вектора равен циркуляции этого вектора по контуру, ограничивающему поверхность.