Теорема Остроградского-Гаусса

Выведем выражение, дающее связь между потоком вектора через некоторую замкнутую поверхность, имеющую конечные размеры, и дивергенцией этого вектора внутри объема, ограниченного данной поверхность. Для вывода разделим объем на части, соприкасающиеся между собой. Для каждой части объема, исходя из приближенного равенства, вытекающего из определения дивергенции, можно записать связь между потоком вектора через поверхность этого частичного объема и дивергенцией вектора внутри объема. 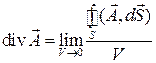Так как , то

,

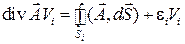где 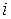− номер частичного объема, 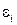− малая величина, которая стремится к нулю вместе с 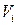. Определение дивергенции дается для бесконечно малого объема, а записанное равенство – для малого, но конечного объема, в связи с чем это равенство отличается от определения дивергенции тем, что введена величина 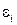, исчезающая при переходе к пределу, когда объем стремится к нулю. Значение 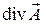здесь взято в некоторой точке внутри частичного объема номера .

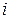Так же, как и при выводе теоремы Стокса, просуммируем выражения такого вида, записанные для всех частичных объемов, на которые разбит конечный объем :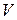

.

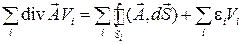Сумма потоков вектора через поверхности всех частичных объемов, на которые был разбит общий объем, представляет собой поток вектора через поверхность всего объема 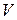(общего), так как птоки по граничным поверхностям, отделяющим друг от друга частичные объемы, направлены в противоположные стороны и взаимно сокращаются. То есть, положительное направление потока в сторону внешней нормали к поверхности оказывается взаимно противоположным для двух соседних объемов, разделенных поверхностью:

.

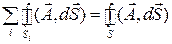Данное равенство сохраняет силу при любом числе частичных объемов.

Заменив сумму потоков на поверхностный интеграл, устремим число частичных объемов к бесконечности, при этом величины самих объемов будут стремиться к нулю. Тогда в пределе сумма в левой части (?) перейдет в интеграл, а последняя сумма в правой части – исчезнет. В результате получится математическая формулировка теоремы Остроградского-Гаусса:

.

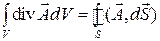Интеграл по объему от дивергенции вектора равен потоку этого вектора через поверхность, окружающую объем.

На этом мы заканчиваем рассмотрение положений векторного анализа и переходим собственно к теории электромагнитного поля.