Ротор, физический смысл ротора
В исследовании движения, например, жидкости, воронки и водовороты на поверхности воды всегда привлекают внимание исследователя. Математическая формулировка вращения жидкости приводит к понятию циркуляции, описанной выше. Продемонстрировать роль циркуляции во вращении жидкости можно следующим образом. Представим себе небольшое колесико с лопастями наподобие колеса водяной мельницы, но очень малых размеров. Предположим, что это колесо подвешено на подшипниках и может вращаться вокруг своей оси. Если мы поместим его в течение ручья, то оно либо будет в покое, либо будет вращаться. При этом пусть колесико целиком погружается в воду во всех случаях. Его вращение будет иметь место тогда, когда скорость течения воды в ручье в том месте, где погружено колесико, меняется от точки к точке пространства. Тогда на лопатки колеса с одной стороны вода набегает с несколько меньшей скоростью, чем с другой, и, под воздействием разности сил, действующих на лопатки с разных сторон, колесико придет во вращение, причем тем быстрее, чем больше неравномерность скорости в месте его погружения.

Рисунок 15 − Ротор
Колесико является лишь своеобразным индикатором вращения частей жидкости. Чтобы математически записать величину, определяющую тенденцию жидкости вращаться, проведем мысленно окружность через центры лопаток колеса и для этого контура, который собой представляет проведенная окружность, запишем циркуляцию скорости жидкости 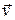 :
:
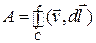 .
.
Если циркуляция равна нулю, то колесико останется неподвижным, если же циркуляция будет положительна, колесико начнет вращаться в положительном направлении, и наоборот. Вектор угловой скорости колесика будет направлен вдоль его оси в правовинтовой системе координат.
Чтобы сделать определение состояния жидкости независимым от размеров колесика, надо рассмотреть предел отношения циркуляции к площади поверхности круга, ограниченного контуром 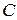 . Это выражение даст проекцию некоторого вектора на направление оси колесика
. Это выражение даст проекцию некоторого вектора на направление оси колесика 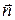 :
:
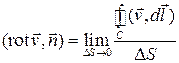
Направление нормали связано с направлением положительного обхода по контуру с правилом правого винта.
Данный вектор называется ротором. Чтобы определить его полностью, нужно найти все три его проекции на взаимно перпендикулярные направления по аналогичным формулам, затем умножить их на соответствующие орты и сложить. Тогда, используя оператор Гамильтона, получим
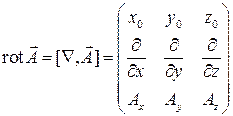
и
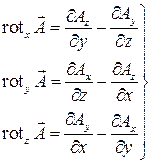
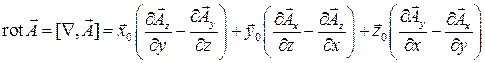
Дата добавления: 2015-10-19; просмотров: 1786;
