Визначення коефіцієнта в’язкості за методом Стокса
Англійський фізик і математик Д.Стокс (1814-1903) досліджував характер сил що діють на тіла що рухаються в рідині і виявив що при невеликих швидкостях руху опір середовища зумовлений практично тільки силами внутрішнього тертя. Сила опору при русі твердого тіла пропорційна швидкості тіла 
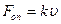 . Коефіцієнт пропорційності
. Коефіцієнт пропорційності 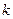 залежить від форми тіла і пропорційний в’язкості рідини і лінійним розмірам тіла. Стокс встановив, що для невеликих кульок, сила опору руху в рідинах дорівнює
залежить від форми тіла і пропорційний в’язкості рідини і лінійним розмірам тіла. Стокс встановив, що для невеликих кульок, сила опору руху в рідинах дорівнює
 ,
,
де  - в'язкість рідини,
- в'язкість рідини,  швидкість руху кульки,
швидкість руху кульки, 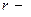 радіус кульки.
радіус кульки.

Рис.5.3
Розглянемо сили, що діють на кульку в рідині. На рис.5.1 показані три сили: сила тяжіння 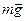 , виштовхуюча сила Архімеда
, виштовхуюча сила Архімеда  і сила опору
і сила опору 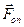 ,яку
,яку  називають силою Стокса. Основний закон динаміки поступального руху кульки
називають силою Стокса. Основний закон динаміки поступального руху кульки 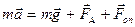 .
.
В проекції навісь 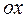 :
:
 . (5.2)
. (5.2)
З трьох сил тільки одна є змінною – це сила опору 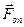 . Дійсно, сила опору пропорційна швидкості кульки, тому спочатку руху швидкість почне зростати. Сила опору (
. Дійсно, сила опору пропорційна швидкості кульки, тому спочатку руху швидкість почне зростати. Сила опору (  ) також буде зростати, а прискорення буде зменшуватись і наступить такий момент, коли прискорення стане дорівнювати нулю. Починаючи з цього моменту кулька буде рухатись рівномірно. Тобто падіння кульки спочатку буде прискореним, а далі кулька рухається з сталою швидкістю (
) також буде зростати, а прискорення буде зменшуватись і наступить такий момент, коли прискорення стане дорівнювати нулю. Починаючи з цього моменту кулька буде рухатись рівномірно. Тобто падіння кульки спочатку буде прискореним, а далі кулька рухається з сталою швидкістю ( 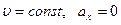 ). Рівняння руху (5.2) буде мати вид:
). Рівняння руху (5.2) буде мати вид:
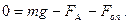
Звідки:
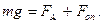 (5.3)
(5.3)
За законом Архімеда виштовхувальна сила дорівнює вазі рідини, яка витісняється кулькою. Об'єм кульки -  густина рідини -
густина рідини - 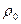 , тому маса рідини яку витісняє кулька
, тому маса рідини яку витісняє кулька 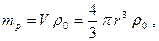 а сила Архімеда
а сила Архімеда  Маса кульки може бути знайдена за формулою
Маса кульки може бути знайдена за формулою 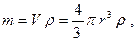 де
де  - густина матеріалу кульки, а сила тяжіння тоді дорівнює
- густина матеріалу кульки, а сила тяжіння тоді дорівнює  . Підставимо отримані значення сил у рівняння (5.3)
. Підставимо отримані значення сил у рівняння (5.3) 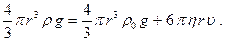
Звідки в'язкість:
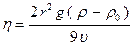 . (5.4)
. (5.4)
Швидкість з якою рухається кулька можна знайти за формулою  де
де  - відстань між двома мітками на посудині, а
- відстань між двома мітками на посудині, а 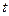 - час, за який кулька проходить цю відстань. Враховуючи, що зручніше вимірювати діаметр кульки
- час, за який кулька проходить цю відстань. Враховуючи, що зручніше вимірювати діаметр кульки  , формулу (5.4 ) можна записати у вигляді:
, формулу (5.4 ) можна записати у вигляді:

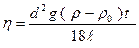 . (5.5)
. (5.5)
Дата добавления: 2015-10-22; просмотров: 744;
