Волновая функция и ее статистический смысл

Экспериментальное подтверждение идеи де Бройля об универсальности корпускулярно-волнового дуализма, ограниченность применения классической механики к микробъектам, диктуемая соотношением неопределенностей, а также противоречие целого ряда экспериментов с применяемыми в начале XX в. теориями привели к новому этапу развития квантовой теории — созданию квантовой механики, описывающей законы движения и взаимодействия микрочастиц с учетом их волновых свойств.

В квантовой механике состояние микрочастиц описывается с помощью волновой функции, которая является основным носителем информации об их корпускулярных и волновых свойствах. Вероятность нахождения частицы в элементе объемом dV равна

dW= │Ψ│² dV. (33.6)

Величина │Ψ│² = dW/dV - имеет смысл плотности вероятности, т.е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с координатами х, у, z. Таким образом, физический смысл имеет не сама Ψ- функция, а квадрат ее модуля |Ψ|², которым задается интенсивность волн де Бройля.

Вероятность найти частицу в момент времени t в конечном объеме V, равна

W= 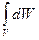= 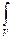│Ψ│² dV. (33.7)

Так как │Ψ│²dV определяется как вероятность, то необходимо волновую функцию Ψ нормировать так, чтобы вероятность достоверного события обращалась в единицу, если за объем V принять бесконечный объем всего пространства. Это означает, что при данном условии частица должна находиться где-то в пространстве. Следовательно, условие нормировки вероятностей

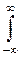│Ψ│² dV =1, (33.8)

где данный интеграл (8) вычисляется по всему бесконечному пространству, т. е. по координатам х, у, z от - ∞ до ∞. Функция Ψ должна быть конечной, однозначной, и непрерывной.