Туннельный эффект

Рассмотрим простейший потенциальный барьер прямоугольной формы (рис.33.2.а) для одномерного (по оси х) движения частицы. Для потенциального барьера прямоугольной формы высоты U ширины l можем записать

0, х < 0(для области 1),

U(x) = {U, 0 ≤ х ≤ l}(для области 2), (33.15)

0, х > 1(для области 3),

При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером (при Е> U), либо отразится от него (при Е< U) и будет двигаться в обратную сторону, т. е. она не может проникнуть сквозь барьер. Для микрочастицы же, даже при Е> U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При Е< U Рис.33.2.

имеется также отличная от нуля вероятность, что частица окажется в области х>l, т. е. проникает сквозь барьер. Подобные, казалось бы, парадоксальные выводы следуют непосредственно из уравнения Шредингера, описывающего микрочастицы при условиях данной задачи.

Таким образом, квантовая механика приводит к специфическому квантовому явлению, получившему название туннельного эффекта, в результате которого микрообъект может «пройти» сквозь потенциальный барьер.

Для описання туннельного эффекта используют понятие коэффициента прозрачности D потенциального барьера, определяемого как отношение плотности потока прошедших частиц к плотности потока падающих.

Решение уравнения Шредингера для прямоугольной потенциального барьера дает формулу для коэффициента прозрачности:

D = D₀ exp( - 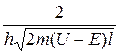), (33.16)

где U — высота потенциального барьера, Е — энергия частицы, l — ширина барьера, D₀— постоянный множитель, который можно приравнять единице. Из этого выражения следует, что D сильно зависит от массы частицы, ширины барьера и от (U - Е); чем шире барьер, тем меньше вероятность прохождения сквозь него частицы.

С классической точки зрения прохождение частицы сквозь потенциальный барьер при Е<U невозможно, так как частица, находясь в области барьера, должна была бы обладать отрицательной кинетической энергией. Туннельный эффект является специфическим квантовым эффектом. Прохождение частицы сквозь область, в которую, согласно законам классической механики, она не может проникнуть, можно пояснить соотношением неопределенностей. Неопределенность импульса Δр на отрезке Δх=l составляет Δp>h/l. Связанная с этим разбросом в значениях импульса кинетическая энергия может сказаться достаточной для того, чтобы полная энергия частицы сказалась больше потенциальной.

Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений физики твердого тела (например, явления в контактном слое на границе двух полупроводников), атомной и ядерной физики (например, a-распад, протекание термоядерных реакций).