Операции над векторами. Скалярное, векторное, смешанное произведение

Векторное исчисление должно ввести ряд операций с векторами и тензорами, как например сложение, умножение, дифференцирование, и изучить эти операции. Эти операции определяются таким образом, чтобы при их помощи легко было интерпретировать те комбинации векторов, которые приходится изучать. В результате как основные элементы векторного исчисления – вектор и тензор, так и операции над ними оказываются хорошо приспособленными для изучения тех физических явлений, в которых большую роль играет направление величин. С одной стороны, это упрощает исследование, с другой, ведет его более естественным и наглядным образом, не требуя введения посторонних элементов.

Рассмотрим, как определяется величина и направление вектора.

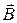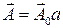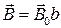Векторы , можно представить как , и , где 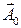, 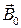− единичные векторы, называемые также ортами, а числа а, b − абсолютные значения векторов , .

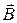Орты, соответствующие направлениям осей x, y, z декартовой координат, будут обозначаться 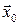, , 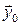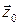(рисунок 2). Любой вектор тогда можно представить в виде разложения 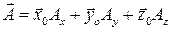, где 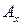, , 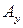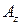являются его проекциями на оси декартовой системы координат. Они также называются компонентами (составляющими) вектора .

Положение какой-либо точки пространства P может быть определено вектором 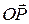, начальной точкой которого служит некоторая, определенным образом выбранная точка O, а концом – точка P. Вектор 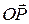мы будем называть радиусом-вектором точки P относительно точки О и будем обозначать обычно как . Про точку P, заданную радиусом-вектором , мы будем говорить, для краткости, что дана точка .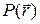

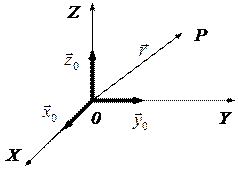
Рисунок 2 − Орты декартовой системы координат и радиус-вектор

Сложение векторов векторов сводится к сложению их компонент:

,

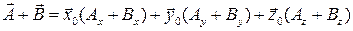эта операция обозначается с помощью обыкновенного знака алгебраического сложения: . Сложение обладает свойством коммутативности: сумма не меняется от перестановки слагаемых: .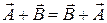

Геометрически это выглядит, как показано на рисунке 3.

Рисунок 3 - Сложение векторов

Скалярное произведение необходимо, например, в механике при вычислении работы, производимой постоянной силой при прямолинейном перемещении и при условии, что сила действует под углом α к перемещению. Работа в этом случае вычисляется как скалярное произведение вектора силы и вектора перемещения. Скалярное произведение двух произвольных векторов определяется как 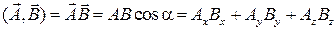, то есть произведение их длин, умноженное на угол между ними (рисунок 4). Результатом скалярного произведения является скаляр.

Рисунок 4 - Скалярное произведение

Векторное произведение. К необходимости рассматривать такую операцию приводят требования геометрического и физического характера.

Векторным произведением векторов и 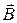называется вектор, по величине равный площади параллелограмма, построенного на векторах и 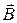, перпендикулярный плоскости этих векторов и направленный в такую сторону, чтобы вращение от к 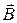на кратчайшем пути вокруг полученного вектора происходило в ту же сторону, как вращение оси x к оси y вокруг оси z (рисунок 5).

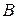
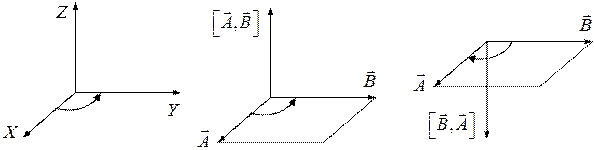
Рисунок 5 − Векторное произведение

Векторное произведение вычисляется как

,

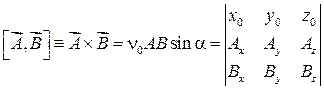тогда компоненты векторного произведения получаются из раскрытия определителя:

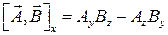
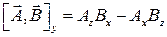
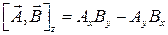
Изменение порядка сомножителей приводит к изменению знака векторного произведения: .

Размерность векторного произведения – единицы измерения площади, т.е. квадратные метры.

Кроме описанных операций сложения, скалярного и векторного произведений, мы будем использовать векторные дифференциальные операторы. Их определение дается позже, непосредственно перед использованием.