Поток вектора
Понятие векторного анализа наиболее наглядны при рассмотрении поля вектора скорости текущей жидкости. Собственно они и возникли в процессе развития гидродинамики, и этим обусловлена терминология, используемая в векторном анализе.
Рассмотрим течение идеальной жидкости, т.е. жидкости несжимаемой, молекулы которой взаимодействуют абсолютно упруго.
По определению, объемжидкости, протекающий в единицу времени через некоторую воображаемую поверхность называется потоком жидкости через S. Пусть скорость направленного движения частиц жидкости, пересекающих поверхность 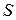 , равна
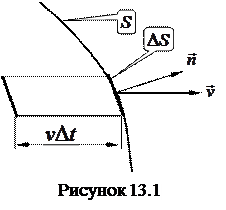
, равна 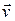 . Выделим мысленно на поверхности элемент
. Выделим мысленно на поверхности элемент 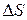 и будем считать, что он настолько мал, что в его пределах скорость направленного движения частиц жидкости одинакова. Ориентацию в пространстве этого элемента зададим ортом нормали к нему
и будем считать, что он настолько мал, что в его пределах скорость направленного движения частиц жидкости одинакова. Ориентацию в пространстве этого элемента зададим ортом нормали к нему 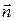 . За время
. За время 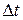 через
через 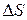 пройдет жидкость, заключенная в объеме
пройдет жидкость, заключенная в объеме

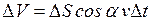 (13.02)
(13.02)
 Следовательно, по определению потока, элементарный поток через
Следовательно, по определению потока, элементарный поток через 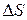 :
:
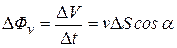 (13.03)
(13.03)
Устремив размеры элемента поверхности 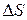 к нулю (
к нулю ( 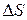 → 0), получим соотношение:
→ 0), получим соотношение:
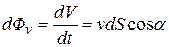 (13.04)
(13.04)
Формула (13.04) в соответствии с определением скалярного произведения векторов эквивалентна следующим:
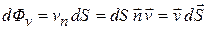 . (13.06)
. (13.06)
Тогда поток жидкости через всю поверхность 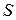 должен определяться соотношением:
должен определяться соотношением:
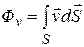 (13.07)
(13.07)
Распространив этот подход на все векторные поля, можем сформулировать определение потока произвольного вектора 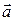 через поверхность
через поверхность 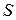 :
:
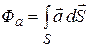 (13.08)
(13.08)
Основные свойства потока вектора: скалярная алгебраическая величина, знак которой зависит от выбора направления нормали к 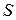 .
.
В случае замкнутых поверхностей всегда используется внешняя нормаль.
Дата добавления: 2015-09-14; просмотров: 1202;
