Циркуляция

Допустим, что неким фантастическим образом мы можем мгновенно заморозить любой объем некоторой движущейся жидкости. И в некоторый момент времени мы мгновенно замораживаем всю жидкость 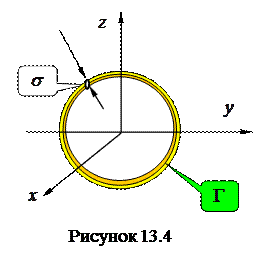, кроме тонкого замкнутого канала постоянного сечения 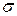, по центру которого проходит контур 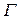. Возникает вопрос: жидкость в канале остановится, или будет двигаться? Если двигаться, то в каком направлении… Очевидно, что результат зависит от характера течения жидкости, с одной стороны, и ориентации в пространстве канала и контура 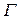. Интуитивно понятно, что если говорить о движении жидкости типа течения реки, когда у дна (за счет взаимодействия с ним) скорость частиц должна быть меньше, чем у поверхности, результат будет зависеть от ориентации в пространстве контура. Если плоскость контура совпадает с направлением течения, и и контур расположен вертикально, то в верхней части контура импульс частиц жидкости больше, и это вызовет вращение жидкости в канале. Если представить контур в горизонтальной плоскости, то жидкость вращаться не будет, и т.д.

Для математического описания задачи примем в качестве меры движения жидкости величину произведения скорости движения жидкости на длину, контура 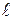: 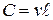, которую называют циркуляцией.

В момент затвердевания у частиц жидкости будет погашена составляющая импульса, перпендикулярная стенкам и останется только тангенциальная составляющая. Жидкость в отрезке длиной 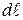будет иметь импульс 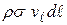. ( 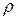- плотность жидкости, 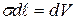- объем элемента контура длиной 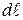, 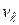проекция скорости частиц жидкости на направление 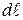). Вследствие идеального взаимодействия частиц жидкости происходит выравнивание их импульсов и жидкость начинает двигаться со скоростью 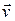. При этом выполняется закон сохранения импульса, так, что импульс жидкости в канале должен быть равен сумме составляющих импульса в элементах канала в направлении контура:

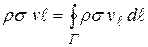, (13.24)

Поэтому циркуляция

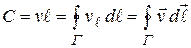(13.25)

В общем случае циркуляцией вектора 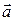по контуру 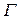называют:

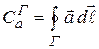(13.26)

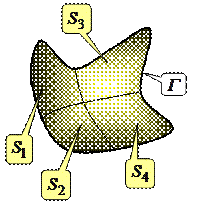Важнейшим свойством циркуляции является ее аддитивность.То есть если некоторая поверхность 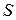, ограниченная контуром 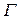разбита на площадки 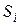то циркуляция по контуру, ограничивающему 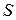равна сумме циркуляций по контурам, ограничивающим :

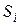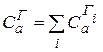(13.27)