Теорема Стокса. Знание в каждой точке поверхности S позволяет найти циркуляцию по контуру Г, ограничивающему S
Знание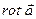 
в каждой точке поверхности S позволяет найти циркуляцию по контуру Г, ограничивающему S. Для этого разобьем S на малые 
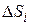, каждую из которых можно считать плоской и описывать вектором 
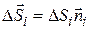. Тогда
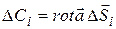. (13.38)
В силу аддитивности циркуляции, циркуляция по контуру Г, ограничивающему S
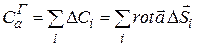. (13.39)
В пределе, при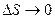 
, учитывая, что 
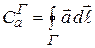, получаем :
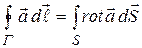. (13.40)
Это соотношение называют теоремой СТОКСА.
13.10 Представление градиента, дивергенции и ротора с использованием оператора Ñ
Запись формул векторного анализа существенно упрощается при использовании векторного дифференциального оператора Ñ:
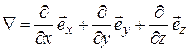. (13.41)
Если Ñ умножить на скалярную функцию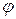 
:
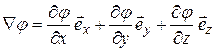, то получаем 
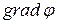. Поэтому часто вместо
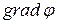пишут 
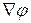. Итак:
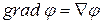. (13.42)
Если Ñ скалярно умножить на векторную функцию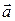 
, то получится скаляр
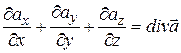. (13.43)
Если же Ñ умножить на вектор 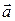векторно, то получим
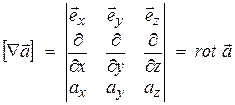. (13.44)
Дата добавления: 2015-09-14; просмотров: 611;