Ротор вектора
Аддитивность циркуляции позволяет ввести понятие об удельной циркуляции, то есть можно рассматривать отношение циркуляции С по контуру ограничивающему S, к величине S: 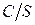 .
.
Для неаддитивной величины рассматривать ее удельную величину бессмысленно. Например, возьмем удельную температуру площадки S: 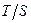 . Температура величина неаддитивная, и от деления площадки на части не меняется. Если площадку разделить на части
. Температура величина неаддитивная, и от деления площадки на части не меняется. Если площадку разделить на части 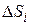 , то их «удельная Т» будет возрастать, при уменьшении
, то их «удельная Т» будет возрастать, при уменьшении 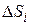 , до бесконечности, ничего не характеризуя. Если взять аддитивную величину массу, то удельная масса площадки в «
, до бесконечности, ничего не характеризуя. Если взять аддитивную величину массу, то удельная масса площадки в « 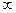 » не уходит, а является поверхностной плотностью площадки, характеризует распределение массы по поверхности. Циркуляция величина аддитивная, и об удельной циркуляции имеет смысл говорить.
» не уходит, а является поверхностной плотностью площадки, характеризует распределение массы по поверхности. Циркуляция величина аддитивная, и об удельной циркуляции имеет смысл говорить.
Однако, удельная циркуляция является макроскопической характеристикой, усреднённо характеризует свойства поля в пределах площадки S. Для описания свойств поля в точке можно использовать удельнную циркуляцию в точке 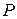 :
:
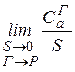 . (13.28)
. (13.28)
Этот предел зависит не только от способности данного поля «создавать» циркуляцию, но и от ориентации в пространстве площадки S, то есть контура ее ограничивающего. Ориентацию контура принято задавать направлением положительной нормали, направление которой связано с направлением обхода контура при вычислении циркуляции, правилом правого винта.
Предел (13.28),найденныйдля противоположно ориентированных положительных 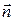 , отличается только знаком. Противоположным направлениям
, отличается только знаком. Противоположным направлениям 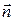 соответствует противоположные
соответствует противоположные 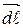 при вычислении
при вычислении 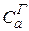 . Существуют такие направления,
. Существуют такие направления, 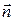 , для которых предел (13.28) достигает максимального значения и такие, когда обращается в нуль.
, для которых предел (13.28) достигает максимального значения и такие, когда обращается в нуль.
Получается, что предел (13.28)ведет себя как проекция некоторого вектора на ось, направленную в сторону нормали, соответствующей максимальному значению предела 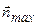 .Если этот вектор направлен в сторону
.Если этот вектор направлен в сторону 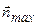 , его проекция максимальна, если он ей перпендикулярен, проекция равна нулю, и проекция отрицательна для направления, противоположного
, его проекция максимальна, если он ей перпендикулярен, проекция равна нулю, и проекция отрицательна для направления, противоположного 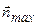 .
.
Этот вектор и называется ротором вектора 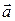 и обозначается
и обозначается
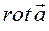 .
.
Максимальное значение предела (13.28)определяет модуль 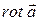 , а соответствующее направление нормали
, а соответствующее направление нормали 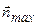 – направление
– направление 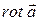 .
.
Таким образом, можно утверждать, что при произвольной ориентации контура предел (13.28) дает проекцию ротора на направление нормали 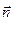 , задающей ориентацию контура в пространстве:
, задающей ориентацию контура в пространстве:
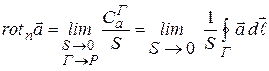 . (13.29)
. (13.29)
13.8 Выражение для 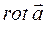 в декартовой системе координат
в декартовой системе координат
 Соотношение (13.29) позволяет найти проекцию ротора вектора на заданное направление. Поскольку
Соотношение (13.29) позволяет найти проекцию ротора вектора на заданное направление. Поскольку 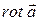 является вектором, для его определения необходимо задать его проекции на оси координат. Это позволит найти вектор в целом:
является вектором, для его определения необходимо задать его проекции на оси координат. Это позволит найти вектор в целом:
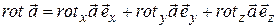 (13.30)
(13.30)
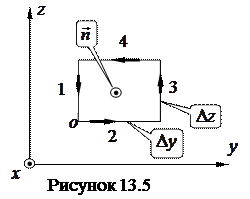
Поэтому представим контур в виде прямоугольника со сторонами, параллельными осям координат 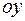 и
и 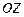 (рисунок 13.5). Выберем направление обхода контура так, как указано стрелками, чтобы нормаль к контуру совпадала с направлением оси
(рисунок 13.5). Выберем направление обхода контура так, как указано стрелками, чтобы нормаль к контуру совпадала с направлением оси 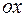 . Площадь контура равна
. Площадь контура равна 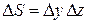 . Найдем циркуляцию по такому контуру и, разделив ее на площадь контура, получим выражение для проекции ротора на ось
. Найдем циркуляцию по такому контуру и, разделив ее на площадь контура, получим выражение для проекции ротора на ось 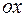 .
.
На участке 1 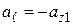 , поскольку на этом участке элементы контура направлены навстречу оси
, поскольку на этом участке элементы контура направлены навстречу оси 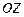 . На участке 3
. На участке 3 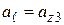 . Аналогичные соотношения справедливы и для участков 2 и 4. Будем считать
. Аналогичные соотношения справедливы и для участков 2 и 4. Будем считать 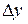 и
и 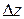 достаточно малыми, чтобы проекцию вектора
достаточно малыми, чтобы проекцию вектора 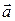 на этих участках можно было бы считать постоянной. Тогда для циркуляции по контуру можно записать:
на этих участках можно было бы считать постоянной. Тогда для циркуляции по контуру можно записать:
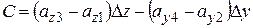 . (13.31)
. (13.31)
Приращение составляющей 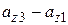 при смещении на
при смещении на 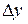 представим в виде:
представим в виде:
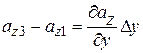 . (13.32)
. (13.32)
Соответственно
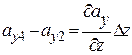 . (13.33)
. (13.33)
Поэтому циркуляция по контуру, ориентированному нормалью вдоль 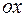 :
:
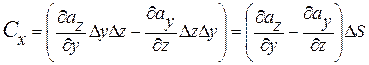 . (13.34)
. (13.34)
Разделим на 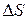 , и для проекции ротора на ось
, и для проекции ротора на ось 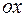 получим:
получим:
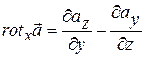 . (13.35)
. (13.35)
Рассуждая аналогичным образом для проекций на 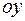 и
и 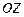 можем записать:
можем записать:
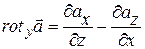 , (13.36)
, (13.36)
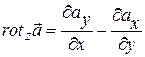 . (13.37)
. (13.37)
Осталось подставить найденные проекции ротора в формулу (13.30):
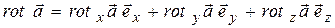 .
.
Дата добавления: 2015-09-14; просмотров: 954;
