Дифференцирование сложных функций
Пусть 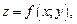 где
где 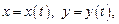 причем
причем  имеет непрерывные частные производные, функции
имеет непрерывные частные производные, функции 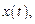
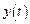 имеют непрерывные производные, t – независимая переменная. Тогда производная сложной функции
имеют непрерывные производные, t – независимая переменная. Тогда производная сложной функции 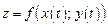 вычисляется по формуле
вычисляется по формуле
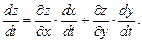 (18.9)
(18.9)
Пусть 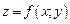 и
и 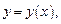 где x – независимая переменная, причем функция
где x – независимая переменная, причем функция  имеет непрерывные частные производные,
имеет непрерывные частные производные, 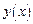 – непрерывную производную. Тогда справедлива формула полной производной функции z по x:
– непрерывную производную. Тогда справедлива формула полной производной функции z по x:
 (18.10)
(18.10)
Пусть  и
и 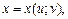
 причем функция
причем функция  имеет непрерывные частые производные по x и y, а функции
имеет непрерывные частые производные по x и y, а функции 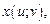
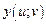 имеют непрерывные частные производные по u и v. Тогда частные производные функции z по u и v находят по формулам:
имеют непрерывные частные производные по u и v. Тогда частные производные функции z по u и v находят по формулам:
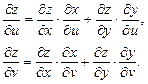 (18.11)
(18.11)
Формулы (18.9)–(18.11) обобщаются на любое конечное количество переменных (зависимых и независимых).
Пример 1. Найти 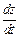 двумя способами (свести к функции одной переменной t и по формуле (18.9)), если
двумя способами (свести к функции одной переменной t и по формуле (18.9)), если  где
где 
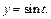
Решение. 1-й способ. Подставив вместо x, y заданные выражения, получим:  – функцию одной переменной t. Тогда
– функцию одной переменной t. Тогда

2-й способ. Найдем частные производные по x и y функции z:


Вычисляем производные функций 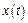 и
и 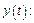


По формуле (18.9) получаем:
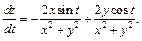
Заменив x и y их выражениями через t, получим:

Пример 2.Вычислить 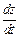 в точке
в точке 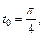 если
если
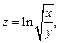 где
где 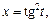
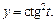
Решение. Находим частные производные заданной функции 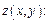
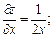
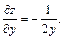
Вычисляем

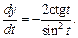
По формуле (18.9) получаем:

Делаем замену переменных:

Вычислим значение 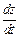 в точке
в точке 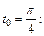

Пример 3. Вычислить различными способами 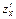 функции
функции  где
где 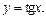
Решение. 1-й способ. Используем метод логарифмического дифференцирования. Прологарифмируем равенство, задающее функцию:
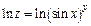 или
или 
Дифференцируем по 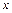 полученное равенство, считая
полученное равенство, считая 
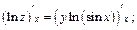
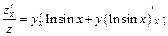

Подставляя вместо z и y заданные выражения из условия, получаем:
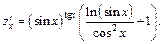
2-й способ. Найдем частные производные:
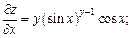
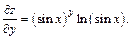
Вычисляем производную функции у:
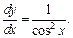
Теперь по формуле (18.10) получаем:
 или
или 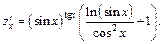
Пример 4.Найти 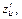
 функции
функции 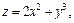 если
если 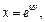
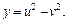
Решение.Используя формулу (18.11), найдем частные производные:
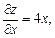
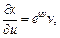
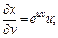
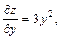
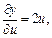
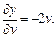
По формуле (18.11) получим:
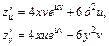 или
или 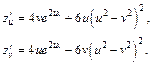
Заметим, что этот пример можно решать и вторым способом – вначале подставить вместо x, y их выражения через u, v, а затем – найти частные производные по u, v.
Пример 5. Найти  функции
функции 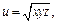 где
где 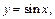
 при
при 
Решение. 1-й способ. Подставив в исходную функцию 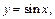
 получим функцию одной переменной:
получим функцию одной переменной:
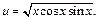
Дифференцируем по x:
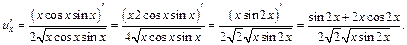
2-й способ. Найдем частные производные:


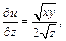
а также производные:
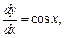
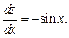
По формуле (18.10) получаем:
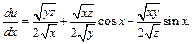
После замены переменных получим:

Пришли к такому же аналитическому выражению для  что и в первом способе решения.
что и в первом способе решения.
Вычислим  в точке
в точке 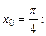
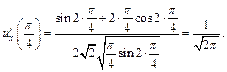
Дата добавления: 2015-09-29; просмотров: 1244;
