Поняття про ферми

Ферма – це шарнірно-стрижневі геометрично незмінні конструкції.

Деякі варіанти таких конструкцій зображені на рис. 69. Область застосування таких конструкцій надзвичайно різноманітна. За своїм призначенням ферми поділяють на:

1. Мостові ферми (рис. 69, а). Вони використовуються при будівництві мостів.

2. Кроквяні ферми (рис. 69, б), які використовуються як каркаси для підтримування покриття будинків і інших споруд.

3. Кранові ферми (рис. 69, в). Вони використовуються в підйомних механізмах.

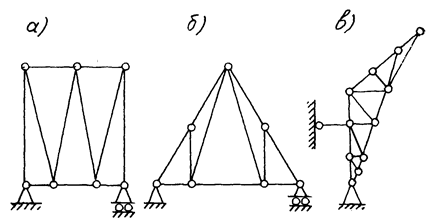
Рис. 69

Ферми поділяються на плоскі і просторові. Якщо всі стрижні ферми лежать в одній площині, то ферма називається плоскою, якщо не лежить в одній площині, то – просторовою. Нижче зупинимося на розгляді плоских ферм.

Визначення ферми як шарнірно стрижневої конструкції є ідеалізованим. В реальних фермах стрижні з’єднані жорстко за допомогою заклепок або електрозварювання. До того ж, в теоретичній механіці на ферми накладають і інші умови, які спрощують їх розрахунок. Такими умовами є:

1. Всі стрижні ферми – прямолінійні.

2. Вагою стрижнів нехтується.

3. Шарніри розміщені тільки на кінцях стрижнів.

4. Самі шарніри, що з’єднують стрижні, є ідеальними, тобто тертям в них нехтується.

5. При розгляді плоских ферм всі сили, що діють на ферму, розміщені в площині ферми і прикладені тільки до її вузлів (шарнірів).

При виконанні даних умов кожний стрижень ферми буде зазнавати зусиль, котрі діють вздовж його осі, тобто стрижні ферми будуть працювати тільки на розтяг або на стиск.

З-поміж всього класу ферм виділимо ферми без зайвих стрижнів.

Якщо конструкція ферми така, що з неї не можна зняти ні одного стрижня, не позбавивши її геометрич-но незмінної конструкції, то така ферми називається фермою без зайвих стрижнів.

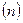Встановимо залежність між кількістю стрижнів і числом вузлів 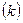плоскої ферми без зайвих стрижнів. Найпростішою геометрично незмінною шарнірно стрижневою конструкцією є трикутник, який складається з трьох стрижнів, що з’єднані між собою шарнірами А, В, С (рис. 70). Для утворення кожного наступного вузла (наприклад, вузла D) необхідно два стрижні. Отже, для утворення 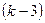вузлів треба 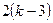стрижнів. Загальна кількість стрижнів 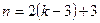. Звідки отримуємо залежність між кількістю стрижнів і числом вузлів для ферми без зайвих стрижнів

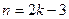. (1.65)

Залежність (1.65) є необхідною умовою жорсткості форми, але не достатньою. Для жорсткості ферми без зайвих стрижнів умова (1.65) повинна виконуватися не лише для всієї ферми, але й для кожної гратки ферми.

Для ферм (рис. 71, а і б) 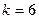, 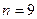і умова (1.65) ( 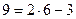) виконується, однак ферма (рис. 71, б) є геометрично змінною. Треба зазначити, що (1.65) є одночасно умовою статичної визначеності ферми.

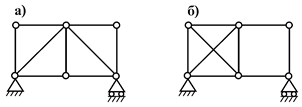
Рис. 71

Статично визначеною називається ферма, котру можна розрахувати методами статики твердого тіла.

Розрахувати ферму в статиці означає розв’язати дві задачі:

1. Визначити реакції опор ферми.

2. Визначити зусилля в усіх стрижнях ферми.

При розв’язуванні першої задачі розглядають ферму як тверде тіло, що перебуває в рівновазі під дією навантажень, які діють на неї, та реакцій опор.

Розв’язування другої задачі базується на положенні: якщо якась конструкція, в нашому випадку ферма, перебуває в рівновазі, то кожний її елемент (стрижень, вузол, частина ферми) також знаходиться в рівновазі. Це дає змогу задачу на визначення зусиль в стрижнях ферми розв’язувати двома способами: способом вирізання вузлів і способом перерізів ферми (спосіб Ріттера).

Спосіб вирізання вузлів

Цей спосіб полягає в тому, що послідовно вирізається кожний вузол ферми і розглядається його рівновага під дією прикладених до нього навантажень, що діють на ферму, та зусиль розрізаних стрижнів. Система сил, що діють на вирізаний вузол, очевидно, буде плоскою системою збіжних сил, рівнова-га якої забезпечується виконанням умов 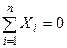, 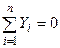або побудовою замкнутого силового багатокутника. Отже, даним способом зусилля в стрижнях ферми можна визначити як аналітично, складаючи рівняння рівноваги, так і геометрично, будуючи замкнуті силові багатокутники. Тут треба пам’ятати, що для плоскої системи сил маємо тільки два рівняння рівноваги, а тому розгляд рівноваги вузлів треба розпочинати з вузла, в якому сходяться тільки два стрижні. Знайшовши зусилля в цих стрижнях, переходять до розгляду рівноваги іншого вузла. Кожний наступний вузол вибирається так, щоб в ньому сходилось не більше двох стрижнів, зусилля в яких невідомі. Тут необхідно знати, що зусилля одного і того ж стрижня на різні вузли за законом дії і протидії діють в протилежні боки.

Розглянувши рівновагу 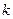-вузлів, отримаємо 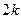рівнянь рівноваги (або побудуємо 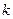замкнутих силових багатокутників), з яких можна отримати 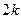невідомих. Оскільки кількість стрижнів ферми визначається формулою (1.65), тобто 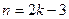, то рівняння рівноваги вузлів ферми дають змогу визначити і опорні реакції. Тобто, визначаючи зусилля в стрижнях ферми способом вирізання вузлів, можна попередньо не визначати опорні реакції. Однак попереднє визначення реакцій опор ферми суттєво спрощує розв’язання задачі на визначення зусиль в стрижнях ферми способом вирізання вузлів.

Спосіб Ріттера

Для застосування цього способу необхідно попередньо визначити опорні реакції. Спосіб Ріттера полягає в тому, що ферму умовно перерізають на дві частини по стрижнях, зусилля в яких треба визначити. Розглядаючи рівновагу однієї з частин ферми під дією прикладених до неї зовнішніх сил, що діють на ферму, та зусиль розрізаних стрижнів, які фактично реалізують дію відкинутої частини ферми на ту, що розглядається, складають відповідні рівняння рівноваги. Оскільки діюча система сил є плоскою, то складають рівняння рівноваги плоскої системи сил (умови (1.52)-(1.53)). Найчастіше вибираються умови (1.53), які полягають в тому, що для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб суми моментів всіх сил системи відносно трьох довільних точок, які знаходяться в площині дії сил і не лежать на одній прямій, дорівнювали нулеві. Такими точками найчастіше вибираються точки попарного перетину розрізаних стрижнів. Ці точки нази-ваються точками Ріттера. Складені таким способом рівняння рівноваги є незв’язаними і дають змогу визначити зусилля в будь-якому стрижні незалежно від зусиль в інших стрижнях.

Якщо два стрижні з трьох розрізаних паралельні, то відповідна точка Ріттера знаходиться в нескінченності. Тоді вибирають умови рівноваги (1.52), тобто складають два рівняння моментів і одне рівняння проекцій сил на вісь, яка перпендикулярна до паралельних стрижнів.