Лема про паралельний перенос сили
З попереднього відомо, що сила – це ковзний вектор. Це положення і аксіома паралелограма сил дали можливість звести до канонічного вигляду систему збіжних сил. Для розширення наших можливостей щодо перетворення системи сил доведемо таку просту теорему (лему):
силу, прикладену до твердого тіла в деякій його точці, можна, не порушуючи її дії на тверде тіло, паралельно перенести в будь-яку точку тіла, якщо при цьому прикласти пару сил, момент якої векторно дорівнює моменту заданої сили відносно точки переносу.
Для доведення цієї теореми розглянемо силу 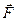 , яка при-кладена в точці
, яка при-кладена в точці 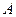 твердого тіла. Візьмемо на тілі довільну точку
твердого тіла. Візьмемо на тілі довільну точку 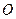 . Радіус-вектор точки
. Радіус-вектор точки 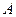 відносно точки
відносно точки 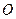 позначимо
позначимо 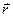 (рис. 37, а). Прикладемо в точці
(рис. 37, а). Прикладемо в точці 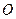 дві сили
дві сили 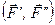 , які вза-ємно зрівноважуються і одна з них, наприклад,
, які вза-ємно зрівноважуються і одна з них, наприклад,  , геометрич-но дорівнює
, геометрич-но дорівнює 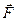 , тобто
, тобто 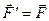 , тоді
, тоді 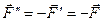 (рис. 37, б). Згідно з аксіомою приєднання і виключення системи зрівноважених сил отримана система сил буде еквівалентною заданій силі
(рис. 37, б). Згідно з аксіомою приєднання і виключення системи зрівноважених сил отримана система сил буде еквівалентною заданій силі 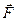
 . (а)
. (а)
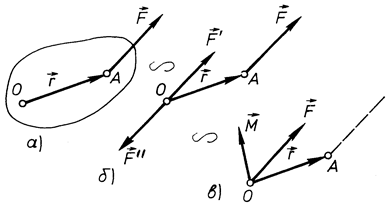
Рис. 37
Оскільки сили 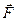 і
і  задовольняють умові
задовольняють умові 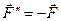 , то ці сили утворюють пару сил, дію якої на тверде тіло можна зобразити моментом
, то ці сили утворюють пару сил, дію якої на тверде тіло можна зобразити моментом 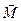 (рис. 37, в). Згідно з попереднім, момент пари сил
(рис. 37, в). Згідно з попереднім, момент пари сил 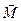 геометрично дорівнює моменту однієї сили пари (наприклад,
геометрично дорівнює моменту однієї сили пари (наприклад, 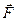 ) відносно точки прикладання іншої сили пари, тобто
) відносно точки прикладання іншої сили пари, тобто
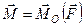 . (б)
. (б)
Отже,
при паралельному переносі сили ( 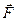 ) в довільну точ-ку отримуємо силу (
) в довільну точ-ку отримуємо силу (  ), геометрично рівну заданій силі, і пару сил , момент якої геометрично дорівнює моменту заданої сили відносно точки переносу.
), геометрично рівну заданій силі, і пару сил , момент якої геометрично дорівнює моменту заданої сили відносно точки переносу.
Зауважимо, що в літературі точку 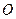 , куди переноситься сила, часто називають точкою зведення, а пару сил, яка при цьому утворюється, називають приєднаною парою. Якщо точка зведення буде знаходитись на лінії дії сили, то момент приєднаної пари буде дорівнювати нулеві, отже, пари сил фактично не буде, тоді ми отримаємо тільки одну силу, тобто ще раз переконуємось, що сила – це ковзний вектор.
, куди переноситься сила, часто називають точкою зведення, а пару сил, яка при цьому утворюється, називають приєднаною парою. Якщо точка зведення буде знаходитись на лінії дії сили, то момент приєднаної пари буде дорівнювати нулеві, отже, пари сил фактично не буде, тоді ми отримаємо тільки одну силу, тобто ще раз переконуємось, що сила – це ковзний вектор.
§ 20 Зведення довільної системи сил
до заданого центра
Дано систему сил 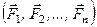 , що прикладені в точках
, що прикладені в точках 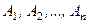 і як завгодно напрямлені в просторі (рис. 38, а). Візьмемо довільну точку
і як завгодно напрямлені в просторі (рис. 38, а). Візьмемо довільну точку 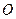 , яку назвемо центром зведення, і зведемо всі задані сили до точки
, яку назвемо центром зведення, і зведемо всі задані сили до точки 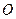 . Згідно з лемою про паралельний перенос сили отримаємо
. Згідно з лемою про паралельний перенос сили отримаємо
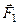
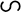
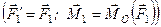 ;
;
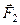
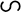
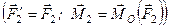 ;
;
. . . . . . . . . . . . . . . . . .
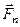
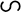
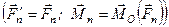 .
.
Отже, в точці 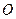 одержано систему сил
одержано систему сил 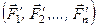 і систему пар сил з моментами
і систему пар сил з моментами 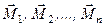 (рис. 38, б). Одержана система сил є збіжною, бо всі сили прикладені до однієї точки
(рис. 38, б). Одержана система сил є збіжною, бо всі сили прикладені до однієї точки 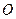 . Геометрично склавши ці сили, знайдемо їх рівнодійну (рис. 39)
. Геометрично склавши ці сили, знайдемо їх рівнодійну (рис. 39)
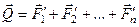 .
.
Оскільки 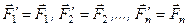 , то отримаємо
, то отримаємо
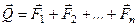 .
.
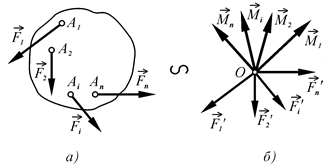
Рис. 38
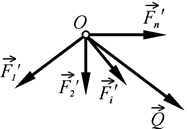 Рис. 39
Рис. 39
| 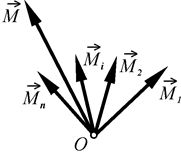 Рис. 40
Рис. 40
|
В отриманій рівності праворуч маємо геометричну суму всіх сил заданої системи, а це, як відомо (див. формулу 1.26), є її головний вектор. Отже, рівнодійна отриманої системи сил геометрично дорівнює головному вектору заданої системи сил 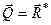 .
.
Систему отриманих пар сил замінимо еквівалентною парою, момент якої, як відомо з теореми про складання пар, дорівнює геометричній сумі моментів складових пар (рис. 40)
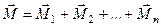 .
.
Оскільки 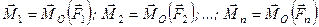 , то отримаємо
, то отримаємо
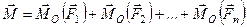 .
.
В отриманій рівності праворуч маємо геометричну суму моментів всіх сил заданої системи відносно точки 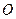 , тобто її головний момент відносно точки
, тобто її головний момент відносно точки 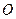 . Отже, момент пари сил, яка еквівалентна отриманій системі приєднаних пар, геометрично дорівнює головному моменту заданої системи відносно точки зведення
. Отже, момент пари сил, яка еквівалентна отриманій системі приєднаних пар, геометрично дорівнює головному моменту заданої системи відносно точки зведення 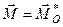 .
.
Таким чином, при зведенні довільної системи сил до заданого центра в даному центрі отримаємо одну силу, яка геометрично дорівнює головному вектору заданої системи сил, і пару сил, момент якої геометрично дорівнює головному моменту заданої системи сил відносно точки зведення (рис. 41).
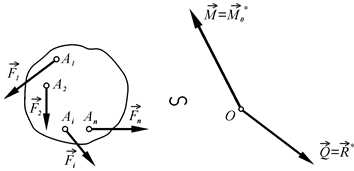
Рис. 41
Тобто, систему сил, розміщених довільно в просторі, завжди можна звести до однієї сили, яка дорівнює її головному вектору і прикладена в точці зведення, і до пари сил, момент якої геометрично дорівнює головному моменту системи відносно точки зведення
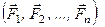
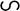
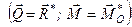 . (1.43)
. (1.43)
§ 21 Окремі випадки зведення довільної системи сил
Зводячи довільну просторову системи сил 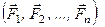 до заданого центра, можемо зустрітись з одним з чотирьох випадків.
до заданого центра, можемо зустрітись з одним з чотирьох випадків.
1. Головний вектор і головний момент заданої системи сил відповідно дорівнюють нулеві
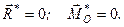 (1.44)
(1.44)
В цьому випадку згідно з еквівалентністю (1.43) маємо
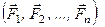
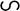
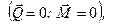
тобто,
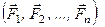
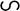 0,
0,
дія заданої системи сил на тверде тіло еквівалентна нулеві, а це означає, що вона є зрівноваженою. Отже, рівності (1.44) є векторними умовами зрівноваження довільної системи сил, які формулюються так:
для рівноваги довільної системи сил необхідно і достатньо, щоб її головний вектор і головний момент дорівнювали нулеві.
2. Головний вектор заданої системи сил дорівнює нулеві 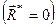 , а головний її момент не дорівнює нулеві
, а головний її момент не дорівнює нулеві 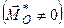 . В цьому випадку система сил зводиться до пари сил, момент якої дорівнює головному моменту
. В цьому випадку система сил зводиться до пари сил, момент якої дорівнює головному моменту 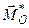 заданої системи сил відносно центра зведення
заданої системи сил відносно центра зведення 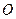 , тобто, геометричній сумі моментів всіх сил системи відносно центра зведення.
, тобто, геометричній сумі моментів всіх сил системи відносно центра зведення.
3. Припустимо тепер, що головний вектор системи сил не дорівнює нулеві 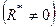 , а головний момент її дорівнює нулеві
, а головний момент її дорівнює нулеві 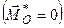 . В цьому випадку у відповідності з (1.43)
. В цьому випадку у відповідності з (1.43)
маємо
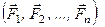
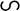
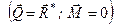 ,
,
тобто
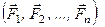
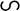
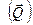 .
.
Але, якщо деяка система сил зводиться до однієї сили, то ця сила називається рівнодійною.
Отже, в даному випадку система сил зводиться до рівнодійної 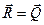 , яка прикладена в центрі зведення і геометрично рівна головному вектору системи.
, яка прикладена в центрі зведення і геометрично рівна головному вектору системи.
4. Нехай головний вектор і головний момент системи не дорівнюють нулеві 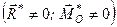 . Тут можуть бути два випадки:
. Тут можуть бути два випадки:
а). Головний вектор і головний момент взаємно перпендикулярні 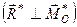 .
.
В цьому випадку відносно центра зведення О (рис. 42) маємо силу 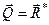 і пару сил з моментом
і пару сил з моментом 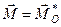 . До того ж вектор моменту пари буде перпендикулярний до вектора сили
. До того ж вектор моменту пари буде перпендикулярний до вектора сили  . Отриману систему можна спростити. Для цього вектор моменту пари
. Отриману систему можна спростити. Для цього вектор моменту пари 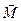 зобразимо парою, яку розмістимо так, щоб одна з сил пари (сила
зобразимо парою, яку розмістимо так, щоб одна з сил пари (сила 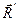 на рис. 43) була прикладена в бік, протилежний напряму сили
на рис. 43) була прикладена в бік, протилежний напряму сили  . Візьмемо сили
. Візьмемо сили 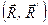 , які становлять пару, чисельно рівними силі
, які становлять пару, чисельно рівними силі 
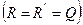 , тоді плече цієї пари братимемо рівним
, тоді плече цієї пари братимемо рівним  . Дві сили
. Дві сили  і
і 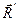 , які прикладені в точці О, взаємно зрівноважуються і їх можна виключити, в результаті чого залишиться одна сила
, які прикладені в точці О, взаємно зрівноважуються і їх можна виключити, в результаті чого залишиться одна сила 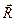 , прикладена в точці С (рис. 44). Отже, в цьому випадку система сил зводиться до однієї сили, тобто до рівнодійної, геометрично рівної головному вектору системи. Точка прикладання рівнодійної (точка С) зміщена від центра зведення системи (точки О) на відрізок ОС, який визначається за формулою
, прикладена в точці С (рис. 44). Отже, в цьому випадку система сил зводиться до однієї сили, тобто до рівнодійної, геометрично рівної головному вектору системи. Точка прикладання рівнодійної (точка С) зміщена від центра зведення системи (точки О) на відрізок ОС, який визначається за формулою
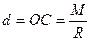 , (а)
, (а)
де 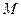 – момент пари сил, отриманий при зведенні системи сил до центра О (рис. 42);
– момент пари сил, отриманий при зведенні системи сил до центра О (рис. 42); 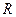 – отримана рівнодійна. Оскільки
– отримана рівнодійна. Оскільки 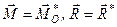 , то відношення (а) можна записати у вигляді
, то відношення (а) можна записати у вигляді
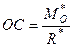 , (1.45)
, (1.45)
  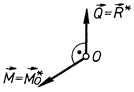 Рис. 42
Рис. 42
| 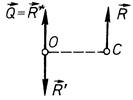 Рис. 43
Рис. 43
| 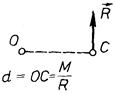 Рис. 44
Рис. 44
|
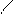 б). Головний вектор і головний момент не є взаємно перпендикулярними
б). Головний вектор і головний момент не є взаємно перпендикулярними 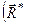 ^
^ 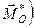 .
.
В цьому випадку відносно центра зведення О (рис. 45) маємо силу 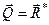 і пару сил з моментом
і пару сил з моментом 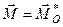 . До того ж вектор моменту пари утворює деякий кут
. До того ж вектор моменту пари утворює деякий кут 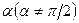 з вектором сили
з вектором сили  . Це найбільш загальний випадок зведення довільної системи сил до заданого центра.
. Це найбільш загальний випадок зведення довільної системи сил до заданого центра.
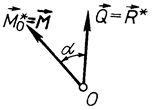 Рис. 45
Рис. 45
| 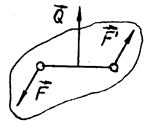 Рис. 46
Рис. 46
|
Подальше спрощення отриманої системи сил можна провести в двох напрямах. Її можна звести до двох мимобіжних сил або звести до силового гвинта (динами).
Силовим гвинтом (динамою) називається система сил, яка складається з пари сил і сили, яка перпендикулярна до площини дії пари (рис. 46).
Тут ми розглянемо зведення системи сил до силового гвинта. Для цього момент отриманої пари сил (рис. 45) розкладемо на дві складові (рис. 47, а)
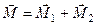 .
.
Величини цих складових
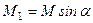 ;
; 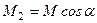 ,
,
і їх напрями: 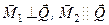 . Вектор моменту
. Вектор моменту 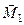 зобразимо парою сил
зобразимо парою сил 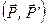 , причому візьмемо сили пари рівними за ве-личиною силі
, причому візьмемо сили пари рівними за ве-личиною силі  і розмістимо цю пару так, щоб одна з цих сил (наприклад,
і розмістимо цю пару так, щоб одна з цих сил (наприклад, 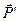 ), була прикладена в точці О і напрямлена протилежно силі
), була прикладена в точці О і напрямлена протилежно силі  (рис. 47, б). Друга сила пари
(рис. 47, б). Друга сила пари 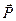 буде прикладена в точці А, яка лежить на перпендикулярі, поставленому в точці О до площини, що проходить через
буде прикладена в точці А, яка лежить на перпендикулярі, поставленому в точці О до площини, що проходить через  і
і 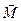 на відстані
на відстані
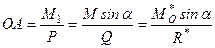 .
.
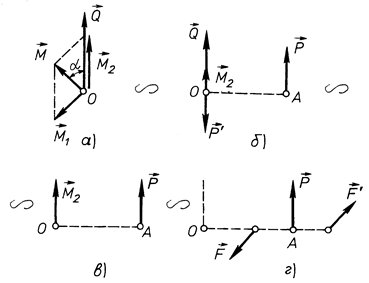
Рис. 47
Дві сили  і
і 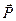 , які прикладені в точці О, взаємно зрівноважуються і їх можна виключити. Залишається сила
, які прикладені в точці О, взаємно зрівноважуються і їх можна виключити. Залишається сила 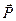 , прикладена в точці А і пара сил з моментом
, прикладена в точці А і пара сил з моментом 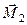 (рис. 47, в). Оскільки момент пари сил є вільним вектором, то перенесемо його в точку А і зобразимо його парою сил
(рис. 47, в). Оскільки момент пари сил є вільним вектором, то перенесемо його в точку А і зобразимо його парою сил 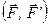 , площина дії якої перпендикулярна моменту
, площина дії якої перпендикулярна моменту 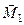 , а значить і силі
, а значить і силі 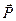 , тобто отримали динаму (рис. 47, г)
, тобто отримали динаму (рис. 47, г)
Пряма, по якій діє сила динами, називається централь-ною віссю системи.
Точки центральної осі системи характеризуються тим, що коли довільну систему сил звести до будь-якої точки центральної осі системи, то отримаємо силу, геометрично рівну головному вектору даної системи і напрямлену вздовж центральної осі, та пару сил, момент якої також напрямлений вздовж центральної осі. Можна легко довести (додаток 5), що момент пари динами дорівнює найменшому значенню головного моменту системи.
Складемо тепер таблицю всіх можливих випадків зведення довільної системи сил до канонічного вигляду.
| № | Значення | Канонічний вигляд (випадок зведення) | ||
| головного вектора | головного моменту | їх скалярного добутку | ||
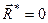
| 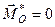
| 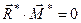
| Система сил еквівалентна нулеві (є зрівноваженою) | |
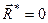
| 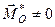
| 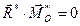
| Пара сил | |
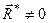
| 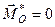
| 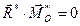
| Рівнодійна, яка прикладена в точці зведення | |
| а) | 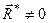
| 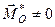 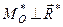
| 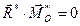
| Рівнодійна, яка зміщена від центра зведення |
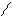 б) б)
| 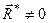
| 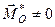 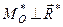
| 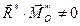
| Динама або дві мимобіжні сили |
Розглянемо тепер частковий випадок – плоску систему сил. Площину, в якій знаходяться сили, позначимо 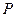 (рис. 48). Геометрично додавши всі сили системи, знаходимо її головний вектор
(рис. 48). Геометрично додавши всі сили системи, знаходимо її головний вектор 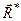 , який, очевидно, буде знаходитись в площині дії сил
, який, очевидно, буде знаходитись в площині дії сил
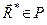 .
.
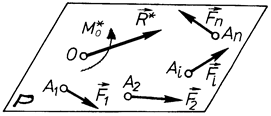
Рис. 48
Вектор моменту кожної сили заданої системи відносно будь-якої точки О площини дії сил буде перпендикулярним до цієї площини, тобто вони утворюють систему паралельних векторів. Тому можна сказати, що
головний момент плоскої системи сил відносно довільної точки площини дії сил дорівнює сумі алгебраїчних моментів всіх сил системи відносно даної точки
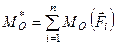 . (1.46)
. (1.46)
Напрям його перпендикулярний до площини дії сили, отже, 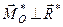 , тобто скалярний добуток головного вектора на головний момент плоскої системи сил завжди дорівнює нулеві:
, тобто скалярний добуток головного вектора на головний момент плоскої системи сил завжди дорівнює нулеві: 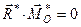 . Це означає, що плоска система сил може мати тільки три випадки зведення – звестись до нуля, тобто бути зрівноваженою; до пари сил; до рівнодійної. Плоска система сил не може звестись до динами.
. Це означає, що плоска система сил може мати тільки три випадки зведення – звестись до нуля, тобто бути зрівноваженою; до пари сил; до рівнодійної. Плоска система сил не може звестись до динами.
§ 22 Інваріанти довільної системи сил
Величини, які не змінюються при певних перетвореннях, називаються інваріантами відносно даних перетво-рень.
Інваріантами довільної системи сил називаються величин, які не залежать від вибору центра зведення. Для встановлення таких величин розглянемо довільну систему сил 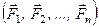 і виберемо дві довільні точки О1 і О2 (рис.
і виберемо дві довільні точки О1 і О2 (рис.
49, а). Звівши систему сил до центра О1, отримаємо (рис. 49, б)
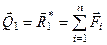 ; (а)
; (а)
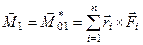 . (б)
. (б)
Якщо задану систему сил звести до центра О2, то в даній точці отримаємо (рис. 49, б)
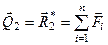 ; (в)
; (в)
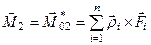 . (г)
. (г)
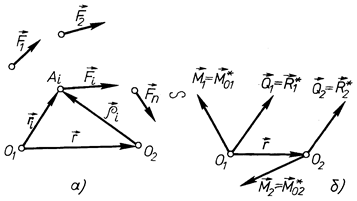
Рис. 49
В рівностях (а) і (в) справа знаходиться геометрична сума однієї і тієї ж системи сил, отже 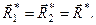
Головний вектор системи сил не залежить від центра зведення, тобто є інваріантом.
Якщо порівняти рівності (б) і (г), то (враховуючи, що 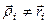 ) можна стверджувати, що головний момент системи сил взагалі залежить від центра зведення. Встановимо цю залежність. Враховуючи (див. рис. 49, а), що
) можна стверджувати, що головний момент системи сил взагалі залежить від центра зведення. Встановимо цю залежність. Враховуючи (див. рис. 49, а), що
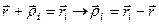 ,
,
отримаємо
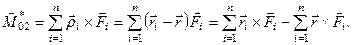
Оскільки (див. рівність б)
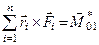 ,
,
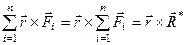 ,
,
то кінцево отримуємо формулу, яка відображає залежність головного моменту системи від центра зведення
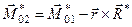 . (1.47)
. (1.47)
При зміні центра зведення головний момент системи зменшується на момент головного вектора, що прикладений в новому центрі зведення відносно старого центра.
Зауваження. В деяких підручниках у формулі (1.47) стоїть знак плюс, це пояснюється тим, що їх автори розглядають момент головного вектора, що прикладений в старому центрі зведення відносно нового центра.
Скалярно помноживши векторну рівність (1.47) на головний вектор 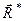
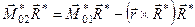
і, враховуючи, що:
а) змішаний добуток 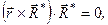 бо в ньому присутні два однакових співмножники
бо в ньому присутні два однакових співмножники 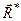 ;
;
б) головний вектор є інваріантом довільної системи сил, тобто 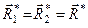 , отримаємо
, отримаємо
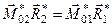 . (1.48)
. (1.48)
Скалярний добуток головного вектора на головний момент не залежить від центра зведення, тобто є інваріантом довільної системи сил.
Таким чином, для довільної системи сил є два інваріанти:
1. Векторний інваріант – це головний вектор довільної системи сил.
2. Скалярний інваріант – це скалярний добуток головного вектора системи сил на її головний момент.
За допомогою формули (1.47) можна провести загальне доведення теореми Варіньйона, яка була доведена для системи збіжних сил. Для цього припустимо, що в точці О2 система зводиться до рівнодійної. Тоді головний момент системи сил відносно точки О2 дорівнює нулеві 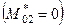 , і рівність (1.47) набуває вигляду
, і рівність (1.47) набуває вигляду
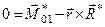
або
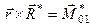 .
.
Враховуючи, що 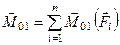 , отримуємо
, отримуємо
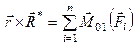 . (д)
. (д)
З другого боку, момент рівнодійної, яка отримується в точці О2 відносно точки О1, визначається за формулою
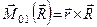 .
.
Оскільки 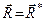 (рівнодійна геометрично рівна головному вектору системи), то отриману рівність можна записати так:
(рівнодійна геометрично рівна головному вектору системи), то отриману рівність можна записати так:
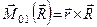 . (г)
. (г)
Враховуючи рівність (д), кінцево отримуємо
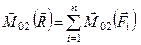 .
.
Отже, теорема Варіньйона доведена для довільної системи сил, яка зводиться до рівнодійної.
§ 23 Аналітичні умови рівноваги
просторової системи сил
Вище (див. § 21) було встановлено, що необхідною і достатньою умовою зрівноваження довільної системи сил є рівність нулеві її головного вектора і головного моменту (див. рівності 1.44)
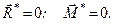 (а)
(а)
Враховуючи, що 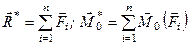 , рівності (а) можна записати у вигляді
, рівності (а) можна записати у вигляді
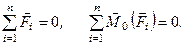 б)
б)
Проектуючи векторні рівності (б) на декартові осі координат, з врахуванням залежності (1.18) отримуємо аналітичні умови рівноваги довільної системи сил
 (1.49)
(1.49)
Отже,
для рівноваги довільної просторової системи сил необхідно і достатньо, щоб сума проекцій всіх сил системи на три координатні осі та суми моментів всіх сил системи відносно цих координатних осей дорівнювали нулеві.
Таким чином, при розв’язуванні задач на рівновагу довільної просторової системи сил, яка прикладена до твердого тіла, необхідно скласти шість рівнянь рівноваги вигляду (1.49) і маємо можливість за їх допомогою визначити шість невідомих величин.
Розглянемо частковий випадок – просторову систему паралельних сил. Систему координат виберемо так, щоб вісь 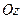 була паралельна лініям дій сил (рис. 50). Система сил буде знаходитись в рівновазі, коли будуть виконуватись умови (1.49), бо це умова рівноваги довільної, тобто будь-якої системи сил. Оскільки розглянута система сил є спрощеним варіантом довільної системи, то і система умов (1.49) повинна спроститись. Спрощення системи (1.49) проведемо шляхом виключення рівностей, які виконуються тотожно, тобто
була паралельна лініям дій сил (рис. 50). Система сил буде знаходитись в рівновазі, коли будуть виконуватись умови (1.49), бо це умова рівноваги довільної, тобто будь-якої системи сил. Оскільки розглянута система сил є спрощеним варіантом довільної системи, то і система умов (1.49) повинна спроститись. Спрощення системи (1.49) проведемо шляхом виключення рівностей, які виконуються тотожно, тобто
фактично є зайвими. Такими рівностями, очевидно, є:
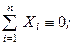
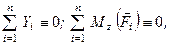 і ми отримуємо систему
і ми отримуємо систему
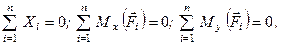 (1.50)
(1.50)
які є аналітичними умовами рівноваги просторової системи паралельних сил.
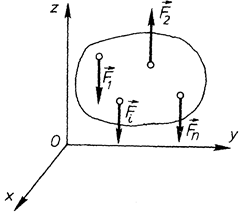
Рис. 50
§ 24 Аналітичні умови рівноваги плоскої системи сил
Розглянемо систему сил, яка розміщена в одній площині (рис. 51). Нехай такою площиною буде площина 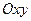 , тобто
, тобто 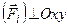 . Розглянута система сил буде зрівноваженою, коли будуть виконуватись умови (1.49), бо, як і було сказано вище, це умови рівноваги будь-якої системи сил. Але розглянута система сил є спрощеним варіантом довільної, отже і система умов (1.49) повинна спроститись. Спрощення проведемо, як і в попередньому випадку, шляхом виключення рівностей, які виконуються тотожно. Такими рівностями є
. Розглянута система сил буде зрівноваженою, коли будуть виконуватись умови (1.49), бо, як і було сказано вище, це умови рівноваги будь-якої системи сил. Але розглянута система сил є спрощеним варіантом довільної, отже і система умов (1.49) повинна спроститись. Спрощення проведемо, як і в попередньому випадку, шляхом виключення рівностей, які виконуються тотожно. Такими рівностями є
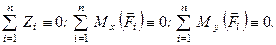
До того ж для даної системи сил, враховуючи, що сили знаходяться в площині, яка перпендикулярна до осі 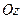 , маємо
, маємо
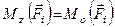 ,
,
і умови (1.49) для плоскої системи сил набувають вигляду
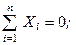

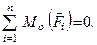 (1.51)
(1.51)
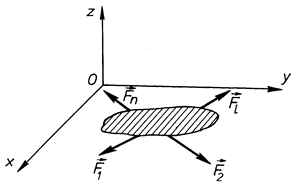
Рис. 51
Для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб суми проекцій всіх сил системи на дві координатні осі та суми їх моментів відносно довільної точки, яка знаходиться в площи-ні дії сил, дорівнювали нулеві.
Таким чином, для плоскої системи сил маємо три аналітичні умови, але їх можна записати в трьох формах. Якщо вва-жати (1.51) умовами рівноваги плоскої системи сил в першій формі, то другою формою її умов рівноваги є
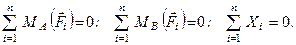 (1.52)
(1.52)
Для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб суми алгебраїчних моментів всіх сил системи відносно двох довільних точок А і В, що знаходяться в площині дії сил, і сума проекцій сил на будь-яку вісь Оx, що лежить в цій площині і не перпендикулярна до прямої, яка з’єднує точки А і В, дорівнювали нулеві.
Третя форма
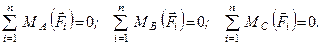 (1.53)
(1.53)
Для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб суми алгебраїчних моментів всіх сил системи відносно трьох довільних точок А, В і С, які знаходяться в площині дії сил і не лежать на одній прямій, дорівнювали нулеві.
При рівновазі плоскої системи сил необхідність виконання умов (1.52) і (1.53) випливає з умов рівноваги (1.51). Доведено достатність цих умов.
В тому, що умови (1.52) і (1.53) є аналітичними умовами рівноваги плоскої системи сил, можна легко переконатися, якщо визначити головний вектор і головний момент плоскої системи сил, котра задовольняє дані умови. Для цього спочатку розглянемо плоску систему сил 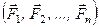 , яка задовольняє умови (1.52) і зведемо дану систему до довільної точки Е (рис. 52). Згідно із загальною теорією зведення системи сил до заданого центра в точці Е отримаємо силу
, яка задовольняє умови (1.52) і зведемо дану систему до довільної точки Е (рис. 52). Згідно із загальною теорією зведення системи сил до заданого центра в точці Е отримаємо силу  , геометрично рівну головному вектору системи
, геометрично рівну головному вектору системи 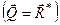 , і пару сил з моментом М, котрий дорівнює головному моменту системи відносно точки зведення
, і пару сил з моментом М, котрий дорівнює головному моменту системи відносно точки зведення 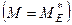 . Оскільки задана система задовольняє умові
. Оскільки задана система задовольняє умові 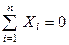 , то її головний вектор, отже і отримана сила, будуть перпендикулярними до осі
, то її головний вектор, отже і отримана сила, будуть перпендикулярними до осі 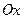 (рис. 52). На площині дії сили вибираємо дві довільні точки А і В і складемо суми моментів сил отриманої системи відносно даних точок (див. рис. 52)
(рис. 52). На площині дії сили вибираємо дві довільні точки А і В і складемо суми моментів сил отриманої системи відносно даних точок (див. рис. 52)
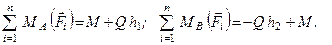
Оскільки 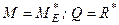 і відповідно до умов (1.52)
і відповідно до умов (1.52) 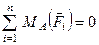 ;
; 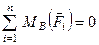 , то отримаємо
, то отримаємо
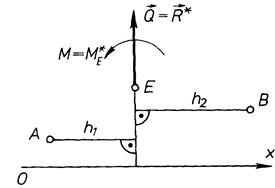
Рис. 52

Звідки 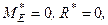 тобто розглянута система сил задовольняє необхідну і достатню умову рівноваги.
тобто розглянута система сил задовольняє необхідну і достатню умову рівноваги.
Тепер розглянемо плоску систему сил, яка задовольняє умови (1.53).Визначимо її головний вектор і головний момент. Для цього систему сил зведемо до центра Е, в якому отримаємо силу 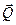 і пару сил з моментом М, причому
і пару сил з моментом М, причому 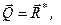
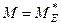 (рис. 53). В площині дії сил вибираємо три довільні точки А, В, С і складаємо суми моментів відносно цих точок. Ці суми згідно з рівняннями (1.53) повинні дорівнювати
(рис. 53). В площині дії сил вибираємо три довільні точки А, В, С і складаємо суми моментів відносно цих точок. Ці суми згідно з рівняннями (1.53) повинні дорівнювати
нулеві.
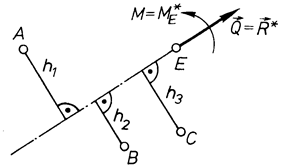
Рис. 53
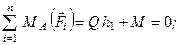
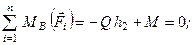
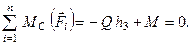
Оскільки в отриманих рівняннях хоча б одне 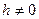 (інакше точки А, В і С будуть знаходитись на одній лінії, що забороняється умовами (1.53)), то отримаємо
(інакше точки А, В і С будуть знаходитись на одній лінії, що забороняється умовами (1.53)), то отримаємо 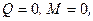 а це означає, що головний вектор і головний момент розглянутої системи відповідно дорівнюють нулеві
а це означає, що головний вектор і головний момент розглянутої системи відповідно дорівнюють нулеві 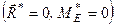 , тобто вона задовольняє необхідній і достатній умові рівноваги.
, тобто вона задовольняє необхідній і достатній умові рівноваги.
Тепер розглянемо частковий випадок плоскої системи сил – плоску систему паралельних сил. Систему координат виберемо так, щоб вісь  була паралельною лініям дій сил (рис. 54). Розглянута система сил буде зрівноважена, коли будуть виконуватись умови (1.51) або (1.52), бо вони є умовами рівноваги будь-якої плоскої системи сил. В даних системах умов перша умова виконується тотожно, тобто
була паралельною лініям дій сил (рис. 54). Розглянута система сил буде зрівноважена, коли будуть виконуватись умови (1.51) або (1.52), бо вони є умовами рівноваги будь-якої плоскої системи сил. В даних системах умов перша умова виконується тотожно, тобто 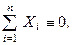 її можна виключити і тоді отримаємо з умов (1.51)
її можна виключити і тоді отримаємо з умов (1.51)
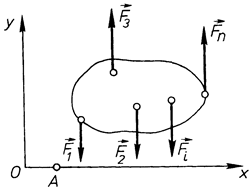
Рис. 54
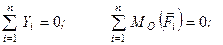 (1.54)
(1.54)
а з умов (1.52)
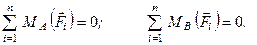 (1.55)
(1.55)
Умови (1.54) і (1.55) є аналітичними умовами рівноваги плоскої системи паралельних сил у двох формах:
Перша форма:
для рівноваги плоскої системи сил необхідно і достатньо, щоб сума проекцій всіх сил системи на вісь, яка паралельна силам, і сума алгебраїчних моментів всіх сил системи відносно довільної точки, що лежить в площині дії сил, дорівнювали нулеві.
Друга форма:
для рівноваги плоскої системи паралельних сил необхідно і достатньо, щоб суми алгебраїчних моментів всіх сил системи відносно двох будь-яких точок А і В, що лежать в площині дії сил і не лежать на прямій, яка паралельна лініям дії сил, дорівнювали нулеві.
Отже, для довільної плоскої системи сил маємо три умови рівноваги, які записані в трьох формах (1.51)–(1.53). Для плоскої системи паралельних сил маємо дві умови рівноваги в двох формах (1.54)–(1.55). Треба зауважити:
1. Система (1.51) є основною формою умов рівноваги довільної плоскої системи сил. Для плоскої системи паралельних сил основною формою умов рівноваги є система (1.54). Це, по-перше, пояснюється тим, що дані умови рівноваги не накладають обмежень на вибір системи координат і точки, відносно якої складається сума моментів. По-друге, скласти суму проекцій сил на вісь, в основному, є легше, ніж скласти суму моментів цих сил відносно точки.
2. Якщо при розв’язанні задачі використовується одна форма умови рівноваги, то для отримання додаткової інформації не треба брати умови рівноваги з другої форми. Коротше кажучи, для довільної плоскої системи сил, що діє на якесь тіло, можна скласти тільки три рівняння рівноваги. Додатково складене рівняння рівноваги ніякої нової інформації не дасть, бо після відповідних перетворень воно співпаде з одним із попередніх рівнянь.
§ 25 Статично означені і статично неозначені задачі
Задачі на рівновагу механічних систем, які розв’язу-ються методами статики твердого тіла, називають-ся статично означеними. В протилежному разі задачі статично неозначені.
Механічні системи, яких це стосується, називаються відповідно статично визначеними і статично невизначеними.
Що означає розв’язати задачу? Розв’язати задачу означає визначити певну кількість невідомих величин. Позначимо К – число невідомих в задачі.
Задачі на рівновагу тіл в статиці розв’язуються методом складання незалежних рівнянь рівноваги. Як відомо з попереднього, кожна система сил має свою кількість умов рівноваги. Позначимо 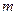 – число незалежних рівнянь рівноваги, які можна скласти для даної системи сил.
– число незалежних рівнянь рівноваги, які можна скласти для даної системи сил.
Очевидно, задача буде статично означеною, якщо
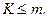 (1.56)
(1.56)
Нерівність (1.56) – це умова статичної означеності задачі. Для різних систем сил ця умова виглядає так:
1. Плоска система збіжних сил 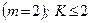 ;
;
2. Плоска система паралельних сил 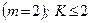 ;
;
3. Довільна плоска система сил 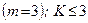 ;
;
4. Довільна просторова система сил 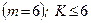 ;
;
5. Просторова система паралельних сил 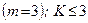 ;
;
6. Просторова система збіжних сил 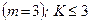 .
.
Як приклад, розглянемо задачу на визначення реакцій в’язей, які накладені на балку АВ, в двох варіантах її закріплення (рис. 55 і 56).
В першому варіанті (рис. 55, а) балка АВ прикріплена до горизонтальної поверхні нерухомим шарніром А і рухомим
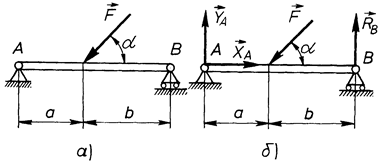
Рис. 55
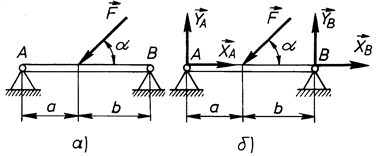
Рис. 56
шарніром В. Оскільки реакція нерухомого циліндричного шарніра має дві складові 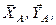 а реакція рухомої опори
а реакція рухомої опори 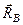 перпендикулярна до опорної поверхні, то в даному варіанті закріплення балки маємо три невідомі:
перпендикулярна до опорної поверхні, то в даному варіанті закріплення балки маємо три невідомі: 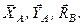 На балку діє плоска система сил, для якої можна скласти три незалежних рівняння рівноваги, отже,
На балку діє плоска система сил, для якої можна скласти три незалежних рівняння рівноваги, отже, 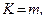 тобто задача є статично означеною.
тобто задача є статично означеною.
Якщо балку АВ прикріпити до горизонтальної поверхні двома нерухомими шарнірами (рис. 56, а), то задача буде статично неозначеною, оскільки число невідомих 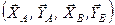 дорівнює чотирьом
дорівнює чотирьом 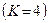 , а для плоскої системи сил, яка діє на балку, можна скласти тільки три незалежних рівняння рівноваги, тобто кількість рівнянь рівноваги, які дає статика, є недостатньою для однозначного визначення всіх реакцій опор. Для розв’язання такої задачі необхідно враховувати пружні властивості тіла АВ, його деформацію, що не входить до компетенції теоретичної механіки. Такі задачі будуть розв’язува-тися в “Опорі матеріалів”.
, а для плоскої системи сил, яка діє на балку, можна скласти тільки три незалежних рівняння рівноваги, тобто кількість рівнянь рівноваги, які дає статика, є недостатньою для однозначного визначення всіх реакцій опор. Для розв’язання такої задачі необхідно враховувати пружні властивості тіла АВ, його деформацію, що не входить до компетенції теоретичної механіки. Такі задачі будуть розв’язува-тися в “Опорі матеріалів”.
Умова статичної означеності задачі (умова 1.56) значно розширюється для систем тіл, що з’єднані між собою і перебувають в рівновазі.
§ 26 Рівновага системи тіл
Розглянемо рівновагу системи тіл, які з’єднані між собою за допомогою шарнірів, гнучких ланок (наприклад, тросів) або вільно спираються одне на одного.
Сили, які діють на таку систему, можна поділити на зовнішні і внутрішні.
Зовнішніми силами називаються сили, з якими тіла системи взаємодіють з тілами, що не входять в дану систему.
Внутрішні сили – це сили взаємодії між тілами однієї і тієї ж системи.
 Треба відразу зазначити, що поділ сил на зовнішні і внутрішні є відносним і залежать від системи тіл, що розглядається. Це означає, що одна і та ж сила для однієї системи тіл є зовнішньою, для іншої системи вона може бути внутрішньою. Так, наприклад, для системи підвішених вантажів (рис. 57, а) зовнішніми силами є:
Треба відразу зазначити, що поділ сил на зовнішні і внутрішні є відносним і залежать від системи тіл, що розглядається. Це означає, що одна і та ж сила для однієї системи тіл є зовнішньою, для іншої системи вона може бути внутрішньою. Так, наприклад, для системи підвішених вантажів (рис. 57, а) зовнішніми силами є: 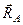 – реакція точки підвісу;
– реакція точки підвісу; 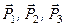 – сили ваги вантажів. Натяги ниток
– сили ваги вантажів. Натяги ниток 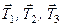 на ділянках АВ, CD, EL утворюють систему внутрішніх сил.
на ділянках АВ, CD, EL утворюють систему внутрішніх сил.
Якщо нитку CD розрізати і розглянути систему двох вантажів (рис. 57, б), то для даної системи зовнішніми силами будуть: 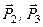 – сили ваги вантажів;
– сили ваги вантажів; 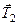 – натяг нитки CD.
– натяг нитки CD.
Отже, сила 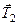 , яка для системи трьох вантажів (рис. 57, а) була внутрішньою, для системи двох вантажів (рис. 57, б) стала зов-нішньою. Другий приклад: сила ваги тіла відносно самого тіла є зовнішньою силою; якщо розглянути систему тіло – Земля, то для даної системи сила ваги тіла буде внутрішньою силою.
, яка для системи трьох вантажів (рис. 57, а) була внутрішньою, для системи двох вантажів (рис. 57, б) стала зов-нішньою. Другий приклад: сила ваги тіла відносно самого тіла є зовнішньою силою; якщо розглянути систему тіло – Земля, то для даної системи сила ваги тіла буде внутрішньою силою.
З наведених прикладів видно, що поділ сил на зовнішні і внутрішні, як було сказано вище, є відносним. Але при розв’язанні кожної задачі такий поділ необхідно чітко проводити, бо внутрішні сили, які прикладені до точок однієї і тієї ж системи (враховуючи, що сили, згідно з законом дії і протидії, виникають попарно) взаємно зрівноважуються.
До того ж з наведеного видно, що внутрішні сили деякої системи тіл можна перевести в зовнішні відносно нової системи, яка є складовою частиною даної системи тіл і отримується в результаті ділення заданої системи тіл. Метод “переве-дення” внутрішніх сил у зовнішні в механіці називається
методом перерізів.
Застосовуючи метод перерізів і враховуючи те, що коли система тіл знаходиться в рівновазі, то кожне тіло даної системи перебуває також в рівновазі; кількість незалежних рівнянь рівноваги, які можна скласти для системи  тіл буде дорівнювати
тіл буде дорівнювати 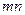 , і задача буде статично означеною, якщо
, і задача буде статично означеною, якщо
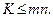 (1.57)
(1.57)
Нерівність (1.57) — це умова статичної означеності задачі для системи  тіл, які перебувають в рівновазі. Так, наприклад, якщо система складається з двох тіл, і на кожне тіло діє довільна плоска система сил, то умова (1.57) набуває вигляду
тіл, які перебувають в рівновазі. Так, наприклад, якщо система складається з двох тіл, і на кожне тіло діє довільна плоска система сил, то умова (1.57) набуває вигляду
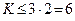 .
.
Примітки:
1. Умова (1.57) справедлива у випадку, коли на тіла системи діють однотипні системи сил. Якщо на тіла системи діють різнотипні системи сил, то умова (1.57) набуває вигляду
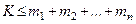 , (1.58)
, (1.58)
де 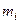 – кількість незалежних рівнянь рівноваги, які можна скласти для системи сил, що діє на і-те тіло.
– кількість незалежних рівнянь рівноваги, які можна скласти для системи сил, що діє на і-те тіло.
2. Число К включає в себе невідомі реакції в’язей, внутрішні зусилля в точках з’єднання тіл, невідомі активні сили і геометричні параметри (відстані, кути і т.ін.).
3. Задачі на рівновагу системи тіл можна розв’язувати двома методами:
3.1. З самого початку розглядається рівновага системи тіл, а пізніше, якщо необхідно, застосовуючи метод перерізів, розглядається рівновага 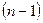 тіла заданої системи і складається необхідна кількість рівнянь рівноваги.
тіла заданої системи і складається необхідна кількість рівнянь рівноваги.
3.2. Застосовуючи метод перерізів, розглядається рівновага кожного тіла системи і складається відповідна кількість рівнянь рівноваги.
Яким методом користуватись? Обидва методи є рівноправними. Тільки можна порекомендувати, якщо в задачі не вимагається визначення зусиль в з’єднувальних елементах системи, то більш ефективним методом розв’язання задачі буде перший метод. Оскільки, розглядаючи рівновагу всієї конст-рукції, в рівняння рівноваги не будуть входити зусилля у з’єд-нувальних елементах, бо вони є внутрішніми силами, невиста-чаючу кількість рівнянь рівноваги отримують шляхом розглядання рівноваги окремих тіл системи і складанням таких рівнянь рівноваги, які не включали б нових, непотрібних для визначення невідомих.
Задача. Два однорідних стрижні однакової довжини з’єднані шарнірно в точці С і шарнірно прикріплені в точках А і В. Вага кожного стрижня 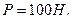 В точці С до стрижня підвішено вантаж
В точці С до стрижня підвішено вантаж 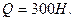 Відстань АВ = а = 1,2 м. Відстань шарніра С до горизонтальної прямої АВ дорівнює
Відстань АВ = а = 1,2 м. Відстань шарніра С до горизонтальної прямої АВ дорівнює 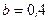 м. Визначити реакції шарнірів А і В (рис. 58, а).
м. Визначити реакції шарнірів А і В (рис. 58, а).
Для розв’язання задачі розглянемо рівновагу всієї конструкції, на яку діють (рис. 58, б):
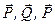 – задані сили;
– задані сили;
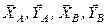 – реакції опор, які необхідно визначити.
– реакції опор, які необхідно визначити.
Діюча система сил є плоскою, рівняннями рівноваги
якої є:
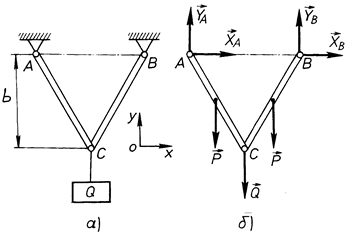
Рис. 58
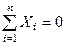 ;
; 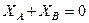 ;
;
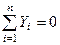 ;
; 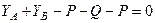 ;
;
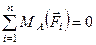 ;
; 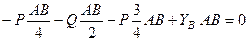 .
.
Підставляючи числові значення, маємо
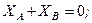
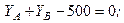
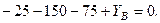
Звідси 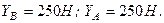
Для знаходження 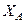 і
і 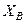 потрібно мати ще рівняння рівноваги. Для отримання цього рівняння розглянемо рівновагу стрижня АС, на який діють (рис. 59)
потрібно мати ще рівняння рівноваги. Для отримання цього рівняння розглянемо рівновагу стрижня АС, на який діють (рис. 59) 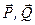 – задані сили;
– задані сили; 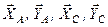 – реакції в’язей.
– реакції в’язей.
 Діюча система сил є плоскою і можна скласти три рівняння рівноваги. Нам для розв’язання задачі потрібно тільки одне рівняння, а тому складемо суму моментів сил відносно точки С, адже тільки це рівняння не включатиме нові невідомі
Діюча система сил є плоскою і можна скласти три рівняння рівноваги. Нам для розв’язання задачі потрібно тільки одне рівняння, а тому складемо суму моментів сил відносно точки С, адже тільки це рівняння не включатиме нові невідомі 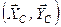
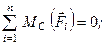
| 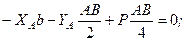
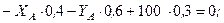
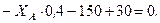
|
Звідси 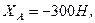 отже,
отже, 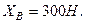
Питання для самоконтролю
1. Яка система сил називається довільною?
2. Що називається головним вектором довільної системи сил?
3. Що називається головним моментом системи сил відносно деякої точки?
4. Як геометрично визначається головний вектор довільної системи сил?
5. Запишіть формули, за допомогою яких аналітично визначається головний вектор довільної системи сил.
 6. Визначіть головний вектор системи сил, яка зображена на рисунку, якщо
6. Визначіть головний вектор системи сил, яка зображена на рисунку, якщо
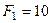 Н,
Н, 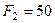 Н,
Н,
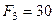 Н,
Н, 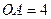 м,
м,
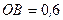 м,
м, 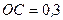 м.
м.
7. Запишіть формули, за допомогою яких аналітично визначається головний момент довільної системи сил відносно деякої точки.
8. Визначіть головний момент системи сил відносно початку координат, яка задана в прикладі № 6.
9. Що називається парою сил?
10. Сформулюйте теорему про момент пари сил відносно довільної точки.
11. Який напрям має вектор моменту пари сил?
12. Запишіть формулу, яка чисельно визначає момент пари сил відносно деякої точки.
13. Які пари сил називається еквівалентними?
14. Сформулюйте теорему про додавання пар сил.
15. До якого канонічного вигляду зводиться система пар сил?
16. Сформулюйте необхідну і достатню умову рівноваги системи пари сил.
17. Запишіть аналітичні умови рівноваги системи пар сил.
18. Сформулюйте лему про паралельний перенос сили в деяку точку.
 19. Силу
19. Силу 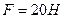 паралельно перенесли з точки К в точку D. Що треба зробити, щоб величини реакцій шарнірів А і В не змінились, якщо
паралельно перенесли з точки К в точку D. Що треба зробити, щоб величини реакцій шарнірів А і В не змінились, якщо 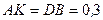 м, KD = 0,4 м ?
м, KD = 0,4 м ?
20. Якщо довільну систему сил звести до деякого центра, що в загальному випадку отримаємо?
21. Коли довільна система сил зводиться до пари сил?
22. В яких випадках канонічним виглядом довільної системи сил є рівнодійна?
23. Що таке динама?
24. Сформулюйте необхідну і достатню умову рівноваги довільної системи сил.
25. Запишіть аналітичні умови рівноваги довільної просторової системи сил.
26. Запишіть аналітичні умови рівноваги довільної плоскої системи сил.
27. В яких формах можна записати аналітичні умови рівноваги довільної плоскої системи сил?
28. Що називається інваріантом довільної системи сил?
29. Які Ви знаєте інваріанти довільної системи сил?
30. Запишіть формулу, яка відображає залежність головного моменту системи сил від центра зведення.
31. Які задачі називаються статично означеними?
32. Як класифікуються сили, що діють на систему тіл, з’єднаних між собою?
33. Задано систему двох тіл, з’єднаних між собою. На одне тіло діє довільна плоска система сил, на інше – плоска система паралельних сил. Скільки найбільше невідомих можна визначити в цій задачі?
1.4 Деякі спеціальні питання статики
В попередніх розділах були розв’язані основні задачі теоретичного курсу статики – це зведення систем до канонічного вигляду і визначення умов (рівнянь) їх зрівноваження. Тепер розглянемо деякі питання, котрі, з одного боку, розширюють коло задач, які розв’язує статика в напрямку їх реальності, а, з другого боку, стануть прикладом практичного застосування от-риманих положень для розв’язування конкретних задач. Одним із напрямків реалізації задач статики є врахування сил тертя.
Опір, що виникає при русі або намаганні рухатися одного тіла по поверхні іншого, називається тертям.
Оскільки найчастіше одне тіло може ковзати або котитись по поверхні іншого тіла, то в теоретичній механіці розглядають два види тертя: тертя ковзання і тертя кочення.
Дата добавления: 2015-06-10; просмотров: 1812;
