Тертя кочення

Опір, який протидіє коченню одного тіла по поверхні іншого, називається тертям кочення.

Для пояснення виникнення цього опору необхідно відійти від традиційно прийнятого в теоретичній механіці поняття “абсолютно тверде тіло”. І дійсно, якщо припустити, що циліндричне тіло і опорна поверхня, на якій воно знаходиться, є абсолютно твердими, то взаємодіятимуть вони по твірній (на плоскому рисунку слідом цієї твірної є точка А), і розподіл сил, які діють на тіло, буде таким, як вказано на рис. 66, де – сила ваги тіла; – сила, яка намагається котити тіло по поверхні; – реакція опорної поверхні, яка розкладена на нормальну складову і горизонтальну (тертя ковзання). Припустимо, що циліндричне тіло перебуває в рівновазі, і складемо рівняння рівноваги. Оскільки на тіло діє плоска система сил, отримаємо

,

,

.

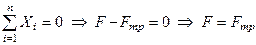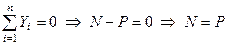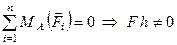Як бачимо, третє рівняння не виконується, а це означає, що під дією будь-якої як завгодно малої сили тіло буде котитись по поверхні. В дійсності цього не спостерігається. Часто треба прикласти значне зусилля, щоб заставити тіло котитись по поверхні. І, як показує практика, величина цього зусилля залежить від пружних властивостей матеріалів циліндричного тіла і опорної поверхні.

Спостереження показують, що в зоні дотику циліндричного тіла і опорної поверхні виникають місцеві деформації тіла і поверхні, внаслідок яких вони взаємодіють по деякій площі шириною “а” (рис. 67, а). Нормальна реакція поверхні буде розподілена за еліптичним законом. При відсутності сили , яка намагається котити тіло по поверхні, цей розподіл буде симетричним, і його рівнодійна, тобто нормальна реакція поверхні , співпаде з лінією дії сили ваги тіла (рис. 67, а).

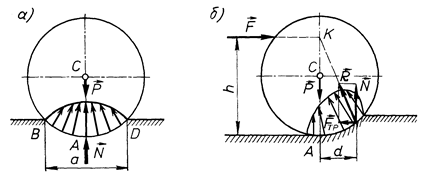
Рис. 67

При прикладанні сили до циліндричного тіла, як вказано на рис. 66, очевидно, тиск тіла на опорну поверхню в зоні АВ (див. рис. 67, а) буде зменшуватись, а в зоні AD – зростати, і інтенсивність реакцій опорної поверхні буде збільшуватись в бік дії сили . Розподіл реакцій опорної поверхні набуває вигляду, як зображено на рис. 67, б. 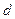При такому розподілі рівнодійна реакція поверхні , буде зміщена в бік дії сили на деяку відстань , і в положенні рівноваги розподіл сил, що діють на циліндр, буде мати вигляд, який зображений на рис. 67, б. При такому розподілі сил, що діють на циліндр, по-перше, задовольняється рівняння моментів

по-друге, цей розподіл задовольняє теорему про три сили.

При рівновазі котка 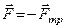і 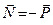, тобто на коток діють дві пари сил. Пара сил 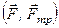намагається котити коток, а пара сил протидіє цьому рухові. Момент пари сил 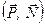називається моментом тертя кочення, і він дорівнює

Величина зміщення 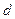буде збільшуватись із зростанням сили . В граничному положенні рівноваги, тобто в момент початку кочення, це зміщення досягне свого максимального значення. Очевидно, це максимальне зміщення буде залежати від фізичних властивостей матеріалів опорної поверхні і циліндричного тіла, тобто є деякою характеристикою цих матеріалів.

Максимальне зміщення нормальної реакції опорної поверхні в бік дії сили при коченні циліндричного тіла називається коефіцієнтом тертя кочення.

Найчастіше коефіцієнт тертя кочення позначається буквою 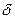, отже . В граничному положенні рівноваги момент тертя кочення досягає свого максимального значення

. (1.63)

Якщо отриману формулу порівняти з формулою (1.60), за допомогою якої розраховується сила тертя ковзання, то побачимо їх схожість. Однак вони мають суттєву відмінність. У формулі (1.60) коефіцієнт тертя ковзання 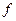є безрозмірною величиною, тоді як коефіцієнт тертя кочення 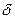має розмірність і, як видно з формули (1.63) і сказаного вище, одиницею вимірювання його є лінійна одиниця, тобто . Експериментально встановлено, що коефіцієнт тертя кочення має такі значення:

1. Сталь по сталі 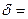5×10^-5 м.

2. Дерево по сталі 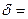(3-4)×10^-4 м.

3. Колесо автомобіля по твердій дорозі 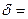2,4×10^-3 м.

На основі рисунка 67, б легко встановити умову чистого кочення. Ковзання буде відсутнє, якщо

.

Оскільки 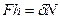, тобто 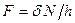, а 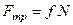, маємо

.

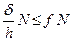Звідси отримаємо

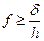, (1.64)

що і є необхідною умовою чистого кочення циліндричного тіла по поверхні. В цій формулі:

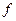– коефіцієнт тертя ковзання;

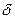– коефіцієнт тертя кочення;

– відстань точки прикладання активної сили від опорної поверхні (див. рис. 68, б).

При розв’язуванні практичних задач реальну модель котка при коченні (рис. 68, а) замінюють розрахунковою (рис. 68, б), яка утворюється шляхом паралельного переносу сил і із точок D в точку А.

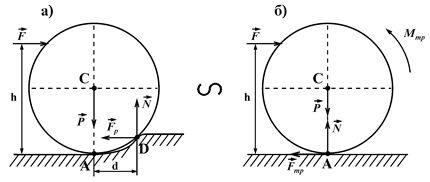
Рис. 68