Коливання при відсутності тертя
Розглянемо випадок параметричного збудження за законом (рис.5.3). Рівняння (5.1) можна переписати у вигляді
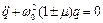 , (5.3)
, (5.3)
де 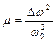 . Так як протягом напівперіоду
. Так як протягом напівперіоду 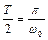 рівняння (5.3) має постійні координати, то можна скористатися способом "зшивання" рішень.
рівняння (5.3) має постійні координати, то можна скористатися способом "зшивання" рішень.
Таким чином, диференціальні рівняння за час 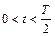 і
і 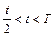 мають відповідно вигляд:
мають відповідно вигляд:
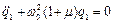 , (5.4)
, (5.4)
і
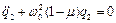 . (5.5)
. (5.5)
Рівняння (5.4) і (5.5) мають рішення:
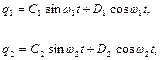 (5.6)
(5.6)
де 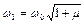 ,
, 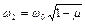 . Для визначення постійних
. Для визначення постійних 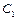 ,
, 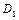 ,
, 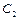 ,
,  сформулюємо початкові умови. Дві умови очевидні: при
сформулюємо початкові умови. Дві умови очевидні: при 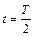 вимоги зшивання запишуться у вигляді:
вимоги зшивання запишуться у вигляді:
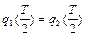 ,
, 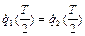 . (5.7)
. (5.7)
Два інших рівності:
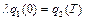 ,
, 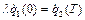 (5.8)
(5.8)
показують, що при закінченні періоду узагальнена координата 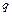 й узагальнена швидкість
й узагальнена швидкість 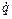 змінилися в
змінилися в 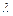 раз. Величина
раз. Величина 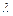 поки невідома.
поки невідома.
Якщо 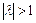 , то коливання в кожному наступному періоді посилюються, а при
, то коливання в кожному наступному періоді посилюються, а при 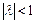 – загасають. Таким чином стійкість системи визначається модулем
– загасають. Таким чином стійкість системи визначається модулем 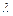 . Підставляючи (5.6) в (5.7) і (5.8), отримуємо однорідну систему алгебраїчних рівнянь, нетривіальне рішення якої вимагає виконання умови
. Підставляючи (5.6) в (5.7) і (5.8), отримуємо однорідну систему алгебраїчних рівнянь, нетривіальне рішення якої вимагає виконання умови
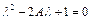 , (5.9)
, (5.9)
де
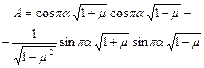 . (5.10)
. (5.10)
Тут 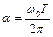 є відношення середнього значення
є відношення середнього значення 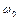 власної частоти системи до частоти пульсацій.
власної частоти системи до частоти пульсацій.
Запишемо корені (5.10)
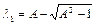 ,
,  . (5.11)
. (5.11)
Щоб 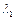 ,
, 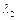 були речовими потрібне виконання умови
були речовими потрібне виконання умови 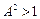 або
або
 , (5.12)
, (5.12)
Тобто 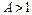 , або
, або 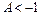 . А значить в обох випадках один з коренів (5.11) більше одиниці. Отже, умова (5.12) являється умовою виникнення параметричного резонансу.
. А значить в обох випадках один з коренів (5.11) більше одиниці. Отже, умова (5.12) являється умовою виникнення параметричного резонансу.
Значення 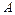 залежить від двох характеристик системи
залежить від двох характеристик системи 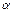 і
і 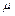 , значення яких і визначають стійкість системи.
, значення яких і визначають стійкість системи.
Діаграма стійкості представлена на рис 5.5 Заштриховані області відповідають стійким станам системи, незаштрихованими - нестійким. З (5.10) при 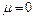 слід
слід
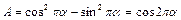
і умова виникнення резонансу 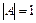 при довільних
при довільних 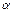 дає
дає  , звідки
, звідки
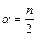 . (5.13)
. (5.13)

Рисунок 5.5 – Діаграма стійкості параметричних коливань в контурі
З (5.13) видно, що коли середнє значення власної частоти вдвічі менше ( 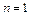 –основне значення) частоти модуляції параметра, параметричний резонанс виникає при скільки завгодно малій глибині параметра збудження.
–основне значення) частоти модуляції параметра, параметричний резонанс виникає при скільки завгодно малій глибині параметра збудження.
Розширення зони нестійкості (див. рис. 5.5) показує, що при збільшенні значення 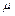 відбудуватися від параметричного резонансу важче; в цьому сенсі він більш небезпечний, ніж звичайний резонанс.
відбудуватися від параметричного резонансу важче; в цьому сенсі він більш небезпечний, ніж звичайний резонанс.
На закінчення відзначимо вплив лінійного тертя на параметричні коливання. Умова виникнення параметричного резонансу стає більш жорсткою, ніж умова (5.12) і означає необхідність певного порогового значення глибини пульсації 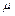 .
.
Дата добавления: 2015-06-12; просмотров: 806;
