Вимушені коливання. У випадку дії на систему сили, яка змінюється по гармонічному закону, коливання описується диференціальним рівнянням (дивись )
У випадку дії на систему сили, яка змінюється по гармонічному закону, коливання описується диференціальним рівнянням (дивись )
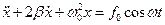 .
.
Тут 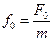 ,
, 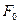 – амплітуда сили,
– амплітуда сили, 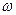 – частота сили. Відмітимо, що в попередньому параграфі
– частота сили. Відмітимо, що в попередньому параграфі 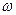 -ою позначалася зовсім інша величина, яку тут позначимо
-ою позначалася зовсім інша величина, яку тут позначимо 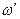 .
.
Рівняння є неоднорідним. Згідно загальний розв’язок неоднорідного рівняння складається із суми загального розв’язку однорідного рівняння і окремого розв’язку неоднорідного рівняння. Загальний розв’язок однорідного рівняння ми знайшли
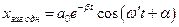 ,
,
де 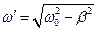 .
.
В пошуках окремого розв’язку неоднорідного рівняння представимо праву частину рівняння комплексним числом
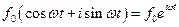 .
.
Приходимо до рівняння
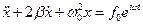 .
.
Окремий розв’язок будемо шукати у вигляді
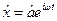
де 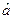 – деяке комплексне число.
– деяке комплексне число.
Диференціюючи по часу
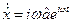 ,
, 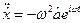
і підставляючи ці вирази в , отримаємо алгебраїчне рівняння
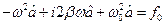 .
.
Звідси
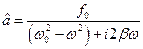 .
.
Запишемо комплексне число, що стоїть в знаменнику, в показниковій формі
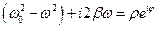
де
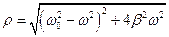 ,
, 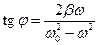 .
.
Підстановкою в одержуємо амплітуду
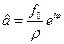 ,
,
а підставляючи в одержуємо окремий розв’язок рівняння
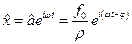 .
.
Дійсна частина цього комплексного числа визначає окремий розв’язок рівняння
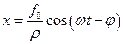 .
.
Тут 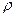 і
і 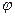 визначаються рівняннями . В загальному розв’язку неоднорідного рівняння , який є сумою рівнянь і , суттєвим є лише рівняння – окремий розв’язок неоднорідного рівняння. Внаслідок експоненціального затухання по закону
визначаються рівняннями . В загальному розв’язку неоднорідного рівняння , який є сумою рівнянь і , суттєвим є лише рівняння – окремий розв’язок неоднорідного рівняння. Внаслідок експоненціального затухання по закону 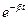 вклад доданка в загальний розв’язок з часом зменшується до нуля. Таким чином, рівняння описує стабільні в часі вимушені коливання.
вклад доданка в загальний розв’язок з часом зменшується до нуля. Таким чином, рівняння описує стабільні в часі вимушені коливання.
Характерною властивістю вимушених коливань є залежність амплітуди коливань 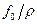 від частоти
від частоти 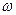 , з якою сила діє на систему, причому ця залежність має максимум. Явище збільшення амплітуди коливань при певній частоті дії сили називається резонансом. Для знаходження резонансної частоти
, з якою сила діє на систему, причому ця залежність має максимум. Явище збільшення амплітуди коливань при певній частоті дії сили називається резонансом. Для знаходження резонансної частоти 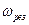 дослідимо на екстремум амплітуду, а точніше функцію
дослідимо на екстремум амплітуду, а точніше функцію 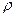 , що стоїть в знаменнику амплітуди .
, що стоїть в знаменнику амплітуди .
Від функції 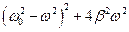 беремо похідну і прирівнюємо її нулю
беремо похідну і прирівнюємо її нулю
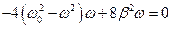 .
.
Це рівняння має три розв’язки: 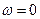 і
і 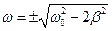 . Розв’язок рівний нулю відповідає мінімуму амплітуди. Із двох інших розв’язків фізичний зміст має розв’язок із знаком „
. Розв’язок рівний нулю відповідає мінімуму амплітуди. Із двох інших розв’язків фізичний зміст має розв’язок із знаком „ 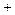 ”. Отже,
”. Отже,
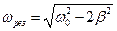 .
.
Підставляючи в рівняння 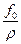 , отримаємо резонансну амплітуду
, отримаємо резонансну амплітуду
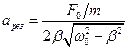 .
.
 Залежності амплітуди вимушених коливань від частоти дії сили для різних значень коефіцієнта затухання
Залежності амплітуди вимушених коливань від частоти дії сили для різних значень коефіцієнта затухання 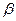 показані на рис.96. У відповідності з і чим менше
показані на рис.96. У відповідності з і чим менше 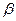 , тим вище і більше зсунутими вправо розташовані на графіках максимуми амплітуди. Із збільшенням частоти амплітуда монотонно зменшується. При зменшенні
, тим вище і більше зсунутими вправо розташовані на графіках максимуми амплітуди. Із збільшенням частоти амплітуда монотонно зменшується. При зменшенні 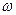 до нуля всі резонансні криві прямують до одного і того ж значення амплітуди
до нуля всі резонансні криві прямують до одного і того ж значення амплітуди 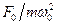 , тобто
, тобто 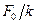 . Це значення дорівнює зміщенню
. Це значення дорівнює зміщенню 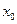 із положення рівноваги, яке отримує система під дією сталої сили величиною
із положення рівноваги, яке отримує система під дією сталої сили величиною 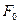 .
.
Дата добавления: 2015-06-17; просмотров: 853;
