Перетворення Лоренца. Чому виникла необхідність у перетвореннях Лоренца і як їх можна було отримати
Чому виникла необхідність у перетвореннях Лоренца і як їх можна було отримати. Щоб відповісти на ці питання, треба ще раз звернутися до хибності уявлень про простір і час, які існували в учнів Ньютона і Галілея. Складність сприйняття нових просторово-часових уявлень спеціальної теорії відносності (СТВ) починається, мабуть, із згадування про ефір. Що таке ефір, якщо потім виявляється, що його просто не існує? Наскільки він (ефір) в свій час був необхідний, зрозуміти це можна, лише ставлячи себе на місце дослідників тих часів і враховуючи ті знання, якими вони володіли. А на той час було добре відомо, як поширюються механічні, звукові хвилі. Звукові хвилі як процес поширення коливань можуть поширюватись лише в якомусь середовищі, не в вакуумі. Коливаються саме частинки середовища. То і світловій хвилі приписували за аналогією ту ж властивість, вважаючи, що світло повинно поширюватись в деякому середовищі, яке і назвали ефіром. В той час було також відомо, що швидкості поширення в твердому тілі повздовжньої і поперечної хвиль визначаються, відповідно, модулем розтягу 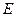 і модулем зсуву
і модулем зсуву 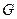 і залежать від густини середовища
і залежать від густини середовища 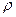 . Обидві швидкості визначаються формулами
. Обидві швидкості визначаються формулами
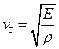 і
і 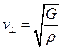 .
.
А враховуючи велику швидкість поширення світла 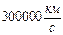 , довелося середовищу, тобто ефіру, в якому світло поширюється, приписати надзвичайні властивості, а саме, що за пружними властивостями він повинен бути твердішим за сталь, а за густиною – розрідженіший за повітря. Але основна помилка була в тому, що світло нібито викликає коливання частинок середовища, ефіру, в якому поширюється. Тобто, про швидкість світла згадувалося, як про швидкість руху матеріальної частинки. Нагадаємо, що в механіці добре відомим є правило додавання швидкостей. Наприклад, якщо відносно якоїсь нерухомої системи відліку рухається платформа (світло) із швидкістю
, довелося середовищу, тобто ефіру, в якому світло поширюється, приписати надзвичайні властивості, а саме, що за пружними властивостями він повинен бути твердішим за сталь, а за густиною – розрідженіший за повітря. Але основна помилка була в тому, що світло нібито викликає коливання частинок середовища, ефіру, в якому поширюється. Тобто, про швидкість світла згадувалося, як про швидкість руху матеріальної частинки. Нагадаємо, що в механіці добре відомим є правило додавання швидкостей. Наприклад, якщо відносно якоїсь нерухомої системи відліку рухається платформа (світло) із швидкістю 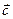 і в тому ж напрямку рухається автомобіль із швидкістю
і в тому ж напрямку рухається автомобіль із швидкістю 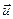 відносно нерухомої системи відліку, то швидкість платформи (світла) відносно автомобіля буде дорівнювати
відносно нерухомої системи відліку, то швидкість платформи (світла) відносно автомобіля буде дорівнювати 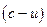 . Так само, гадали, поширюється і світло, якщо спостерігач знаходиться, наприклад, на Землі, яка рухається відносно ефіру із швидкістю
. Так само, гадали, поширюється і світло, якщо спостерігач знаходиться, наприклад, на Землі, яка рухається відносно ефіру із швидкістю 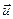 , то світло відносно спостерігача повинно рухатись із швидкістю
, то світло відносно спостерігача повинно рухатись із швидкістю 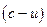 . По суті справи спробам знайти цю різницю швидкостей і були присвячені всі досліди (в тому числі і дослід Майкельсона-Морлі), в яких робилися спроби знайти ту виділену інерціальну систему відліку, яку пов’язали з ефіром. Справді, якщо б виявилося, що відносно автомобіля (див. рис.101) світло мало швидкість
. По суті справи спробам знайти цю різницю швидкостей і були присвячені всі досліди (в тому числі і дослід Майкельсона-Морлі), в яких робилися спроби знайти ту виділену інерціальну систему відліку, яку пов’язали з ефіром. Справді, якщо б виявилося, що відносно автомобіля (див. рис.101) світло мало швидкість 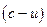 , то
, то  систем відліку, яка віддаляється від автомобіля із швидкістю
систем відліку, яка віддаляється від автомобіля із швидкістю  , була б тією самою виділеною (абсолютною) інерціальною системою відліку. Але виявилося, що ні в одному схожому описаному досліді величина
, була б тією самою виділеною (абсолютною) інерціальною системою відліку. Але виявилося, що ні в одному схожому описаному досліді величина 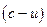 не спостерігалась. Завжди швидкість світла відносно автомобіля була рівною величині
не спостерігалась. Завжди швидкість світла відносно автомобіля була рівною величині 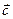 . Експеримент твердив, що природа влаштована так, що вона не дозволяє виділити із усіх якусь особливу інерціальну систему відліку. Висновок: всі інерціальні системи відліку рівноправні в тому розумінні, що фізичні явища, в даному випадку явище поширення світла, протікають в них однаково. Це твердження і було піднесено Ейнштейном в ранг принципу, закону, якому підкоряються властивості оточуючого нас простору. Таким чином, принцип відносності Галілея, що стосувався механічних явищ, був поширений Ейнштейном на всі фізичні явища. Другим принципом спеціальної теорії відносності є твердження про сталість та обмеженість швидкості світла у всіх інерціальних системах відліку.
. Експеримент твердив, що природа влаштована так, що вона не дозволяє виділити із усіх якусь особливу інерціальну систему відліку. Висновок: всі інерціальні системи відліку рівноправні в тому розумінні, що фізичні явища, в даному випадку явище поширення світла, протікають в них однаково. Це твердження і було піднесено Ейнштейном в ранг принципу, закону, якому підкоряються властивості оточуючого нас простору. Таким чином, принцип відносності Галілея, що стосувався механічних явищ, був поширений Ейнштейном на всі фізичні явища. Другим принципом спеціальної теорії відносності є твердження про сталість та обмеженість швидкості світла у всіх інерціальних системах відліку.
Досліди, подібні до експерименту Майкельсона-Морлі, вказали на наближеність перетворень Галілея і на необхідність шукати більш загальні і більш правильні перетворення, якими і виявилися перетворення Лоренца.
 Подивимося на рис.102, на якому показані система відліку
Подивимося на рис.102, на якому показані система відліку 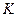 , що є в спокої, й інерціальна система відліку
, що є в спокої, й інерціальна система відліку 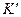 , що рухається рівномірно і прямолінійно (тобто
, що рухається рівномірно і прямолінійно (тобто  ). В момент часу
). В момент часу 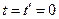 положення обох систем співпадали. Годинники в них синхронізовані, як завжди, за допомогою світлових імпульсів. Нехай в момент часу
положення обох систем співпадали. Годинники в них синхронізовані, як завжди, за допомогою світлових імпульсів. Нехай в момент часу 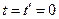 порція світла вийшла із загального співпадаючого початку координат обох систем
порція світла вийшла із загального співпадаючого початку координат обох систем 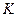 і
і 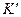 . Нехай точка
. Нехай точка 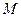 , в яку прийшла порція світла, має в системах
, в яку прийшла порція світла, має в системах 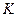 і
і 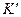 координати відповідно
координати відповідно 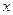 ,
, 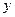 ,
, 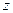 ,
,  і
і 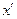 ,
, 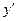 ,
, 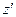 ,
, 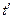 . Згідно з експериментальним результатом про сталість швидкості світла
. Згідно з експериментальним результатом про сталість швидкості світла 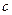 в обох інерціальних системах
в обох інерціальних системах 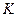 і
і 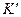 відстані
відстані 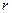 і
і 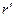 від відповідних початків систем координат до точки
від відповідних початків систем координат до точки 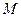 , як видно із рис.102, будуть дорівнювати
, як видно із рис.102, будуть дорівнювати
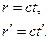
Тому ми вимушені погодитися з тим, що проміжки часу  і
і 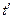 (виміряні різними спостерігачами
(виміряні різними спостерігачами 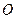 і
і 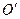 ) різні, хоч це і суперечить нашому повсякденному досвіду.
) різні, хоч це і суперечить нашому повсякденному досвіду.
З формули матимемо
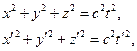
а з міркувань симетрії випливає, що 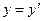 ,
, 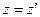 . Таким чином, з формули одержимо:
. Таким чином, з формули одержимо:
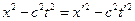 .
.
Припустимо, що формули переходу для координат від одної системи відліку до іншої лінійні і мають наступний вигляд
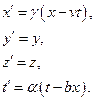
Тут 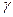 ,
, 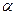 і
і 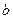 – сталі величини, які ми визначимо пізніше.
– сталі величини, які ми визначимо пізніше.
Формули перетворення повинні задовольняти певні умови: по-перше, бути сумісними з рівнянням . А вимога того, що формули перетворення повинні бути лінійними, задається природно тому, що подія, яка має певні координати в одній системі, повинна перетворюватись в одну подію з іншими координатами другої системи відліку. (Якщо б формули перетворення були, наприклад, квадратичними рівняннями, то, розв’язуючи їх, ми отримали б два розв’язки, які б свідчили про те, що одній події в одній системі відліку відповідали б дві події в другій системі відліку, – неможлива ситуація). Відмітимо, що формули написані в такому вигляді ще і з тих міркувань, що вони повинні задовольняти умову співпадаючих систем, тобто коли 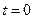 і
і  , то повинна виконуватися умова
, то повинна виконуватися умова 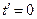 і
і 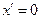 .
.
Підставляючи в , отримаємо:
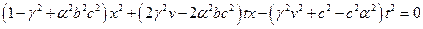 .
.
Оскільки цей вираз тотожньо дорівнює нулю, то
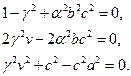
Розв’язуючи цю систему рівнянь відносно 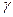 ,
, 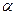 і
і 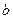 , одержимо:
, одержимо:
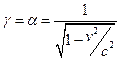 ,
, 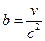 .
.
Формули перетворення , відомі як перетворення Лоренца, можна тепер записати у вигляді:
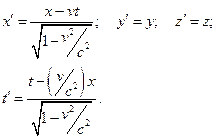
Якщо розв’язати рівняння відносно нештрихованих величин, то отримаємо формули перетворення для переходу від системи 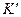 до
до 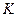 -системи
-системи
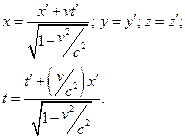
 З перетворень Лоренца випливають незвичайні з точки зору Ньютонівської механіки наслідки. Перший – так зване Лоренцове скорочення довжини. Якщо стержень довжиною
З перетворень Лоренца випливають незвичайні з точки зору Ньютонівської механіки наслідки. Перший – так зване Лоренцове скорочення довжини. Якщо стержень довжиною 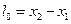 (див. рис.103) знаходиться в стані спокою в
(див. рис.103) знаходиться в стані спокою в 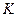 -системі, то для визначення його довжини в рухомій
-системі, то для визначення його довжини в рухомій 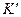 -системі слід відмітити координати його кінців
-системі слід відмітити координати його кінців 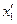 і
і 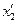 в один і той же момент часу
в один і той же момент часу 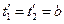 . Різниця
. Різниця 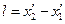 дасть довжину стержня в системі
дасть довжину стержня в системі 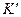 , відносно якої він рухається зі швидкістю
, відносно якої він рухається зі швидкістю 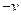 . Використовуючи перше з рівнянь , отримаємо співвідношення
. Використовуючи перше з рівнянь , отримаємо співвідношення
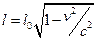 .
.
Таким чином, довжина стержня 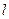 , виміряна в системі, відносно якої він рухається, виявляється меншою, ніж довжина
, виміряна в системі, відносно якої він рухається, виявляється меншою, ніж довжина 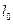 , виміряна в системі, відносно якої стержень знаходиться в спокої.
, виміряна в системі, відносно якої стержень знаходиться в спокої.
Нехай в одній і тій самій точці 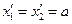 системи
системи 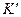 відбуваються дві події. Першій події відповідає момент часу
відбуваються дві події. Першій події відповідає момент часу 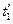 , другій події – момент часу
, другій події – момент часу 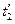 . Згідно з останньою із формул , цим подіям відповідають в системі
. Згідно з останньою із формул , цим подіям відповідають в системі 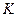 моменти часу
моменти часу
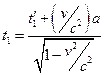 ,
, 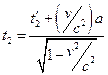 . Звідси
. Звідси 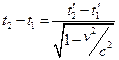 .
.
Вводячи позначення 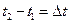 і
і 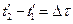 , отримаємо формулу
, отримаємо формулу
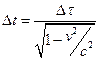 ,
,
яка пов’язує проміжки часу між двома подіями, виміряними в системах 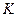 і
і 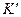 .
.
Припустимо, що обидві події відбуваються з однією частинкою, яка знаходиться в спокої в системі 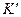 і рухається відносно системи
і рухається відносно системи 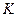 з швидкістю
з швидкістю 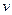 . Тоді
. Тоді 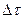 можемо вважати проміжком часу, виміряним за годинником, який рухається разом із частинкою.
можемо вважати проміжком часу, виміряним за годинником, який рухається разом із частинкою. 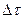 називається власним часом і, як видно з формули , він найменший
називається власним часом і, як видно з формули , він найменший 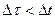 .
.
Співвідношення було експериментально підтверджено, наприклад, в такому досліді. Відомо, що в склад космічних променів входять частки, які називаються 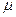 -мезонами, мюонами. Ці частинки нестабільні і розпадаються спонтанно. Середній час життя, виміряний в системі координат, відносно якої
-мезонами, мюонами. Ці частинки нестабільні і розпадаються спонтанно. Середній час життя, виміряний в системі координат, відносно якої 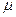 -мезони нерухомі, становить приблизно
-мезони нерухомі, становить приблизно 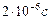 . Здавалось би, що навіть рухаючись зі швидкістю світла,
. Здавалось би, що навіть рухаючись зі швидкістю світла, 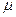 -мезони можуть пройти лише шлях
-мезони можуть пройти лише шлях 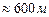 . Однак спостереження показують, що мюони виникають в космічних променях на висоті
. Однак спостереження показують, що мюони виникають в космічних променях на висоті 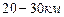 над поверхнею Землі і все ж таки встигають досягти земної поверхні. Цей факт пояснюється тим, що
над поверхнею Землі і все ж таки встигають досягти земної поверхні. Цей факт пояснюється тим, що 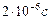 – це власний час життя мюона. Але час, визначений за годинником експериментатора, пов’язаного із Землею, значно більший (див. формулу ). Тому немає нічого дивного в тому, що для земного спостерігача пробіг мюона значно більший, ніж
– це власний час життя мюона. Але час, визначений за годинником експериментатора, пов’язаного із Землею, значно більший (див. формулу ). Тому немає нічого дивного в тому, що для земного спостерігача пробіг мюона значно більший, ніж 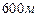 . Відмітимо, що з точки зору спостерігача, який рухається разом із мюоном, відстань, що пролітає
. Відмітимо, що з точки зору спостерігача, який рухається разом із мюоном, відстань, що пролітає 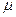 -мезон до поверхні Землі, скорочується згідно з формулою до
-мезон до поверхні Землі, скорочується згідно з формулою до 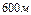 . Тому мюон встигає пролетіти цю відстань за
. Тому мюон встигає пролетіти цю відстань за 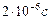 .
.
Цілком природно вважати вирази 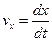 і
і 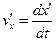 проекціями на осі
проекціями на осі 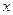 і
і 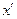 вектора швидкості матеріальної точки відповідно в
вектора швидкості матеріальної точки відповідно в 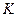 - і
- і 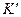 - системах. Із формул випливає, що
- системах. Із формул випливає, що
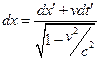 ,
, 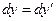 ,
, 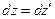 ,
, 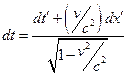 .
.
Поділивши перші три рівності на четверту, одержимо формули перетворення швидкостей при переході від однієї системи відліку до іншої
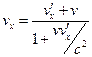 ,
, 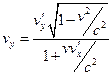 ,
, 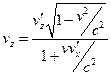 .
.
Із формул легко отримати вирази для швидкостей в системі 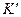 через швидкості в системі
через швидкості в системі 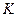 :
:
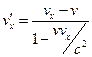 ,
, 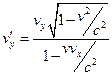 ,
, 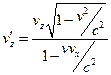 .
.
Ці формули відрізняються від тільки знаком перед 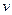 . Якщо тіло рухається паралельно осі
. Якщо тіло рухається паралельно осі 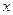 , його швидкість відносно системи
, його швидкість відносно системи 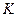 співпадає з
співпадає з 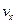 , а швидкість відносно системи
, а швидкість відносно системи 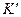 – з
– з 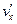 . В цьому випадку закон додавання швидкостей має вигляд
. В цьому випадку закон додавання швидкостей має вигляд
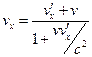 .
.
Нехай швидкість 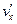 дорівнює швидкості світла
дорівнює швидкості світла 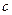 . Тоді для
. Тоді для 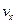 отримаємо за формулою значення
отримаємо за формулою значення
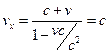 .
.
Припустивши в формулі навіть 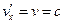 , отримаємо для
, отримаємо для 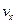 все одно значення, яке дорівнює
все одно значення, яке дорівнює 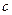 . Таким чином, якщо швидкості
. Таким чином, якщо швидкості 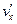 і
і 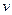 не перевищують
не перевищують 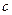 , то і результуюча швидкість
, то і результуюча швидкість 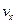 не може перевищити
не може перевищити 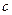 .
.
Дата добавления: 2015-06-17; просмотров: 999;
