Вейвлет-Перетворення

Ідея вейвлет-перетворення складається в розкладанні сигналу ( функції-зображення) по системі функцій, що мають локальний сплеск і швидко убутних на нескінченності [20]. У цьому й наступному параграфах передбачається знайомство читача з базовими поняттями функціонального аналізу (див., наприклад, [3]). Звичайно такі функції вейвлет-перетворення²⁾виводяться з так званого материнського вейвлета. Материнський вейвлет - це функція :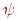

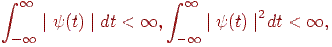
т.е. 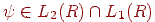; також передбачається, що

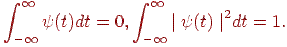
Материнський вейвлет перетворюється в такий спосіб:

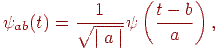
де 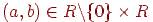. Приклади материнських вейвлетов див. на мал. 14.5. У загальному випадку вейвлет-перетворення записується так:

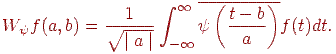
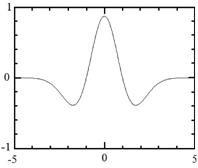
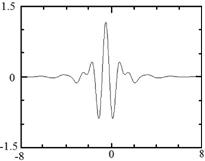
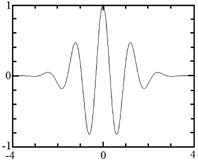
Рис. 14.5. Приклади материнських вейвлетов

При практичному застосуванні вейвлет-перетворення аналіз такого потужного (а саме континуум) безлічі коефіцієнтів неможливий. Тому (a, b) вибираються з рахункової підмножини площини 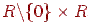. Звичайно материнський вейвлет і безліч значень (a, b) вибирають так, щоб система 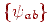утворювала ортонормированный базис у просторі 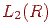. Тоді будь-яку функцію f(x) із цього простору можна розкласти по цьому базисі .

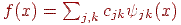Пояснимо як застосовувати вейвлет-перетворення до дискретного сигналу (наприклад, зображенню). Для простоти будемо розглядати одномірний випадок - послідовність кінцевої довжини 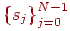. Тоді, за умови що материнський вейвлет 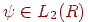, перетворення можна записати так:

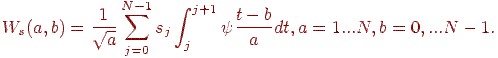
Розглянемо найпростішої вейвлет - вейвлет Хаара (англ. Haar wavelet). Розглянемо простір 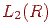. У цьому просторі ортонормированна наступна система:

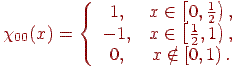
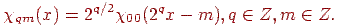
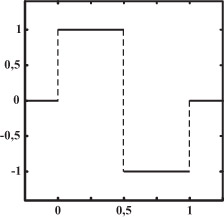
Рис. 14.6. Материнський вейвлет Хаара

Дана система називається системою Хаара. Для такого вейвлета материнським є 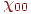(див. мал. 14.6). У цьому випадку (a, b) обрані із 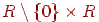за таким законом:

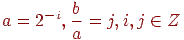
Дія вейвлета Хаара на послідовність, що складається з 2^N елементів, можна розглядати так: елементи групуються по двох, обчислюється сума й різниця кожної пари, різниці зберігаються, а із сум формується послідовність довжини 2 N-¹; далі перетворення виконується доти, поки не залишиться одна сума й відповідно 2^N - 1 різниця. Таке перетворення задається так званою матрицею Хаара:

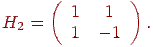
Послідовність (a₀, . . . , a_2N+1) представимо так:

Тепер помножимо праворуч вектори (a_i, a_i+1) на матрицю H₂. Одержимо послідовність сум і різниць ((s₀, d₀), . . . , (s, d)). Якщо послідовність має довжину, кратну 4, то можна застосувати наступну матрицю Хаара:

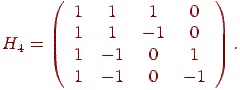
Очевидно, що дані перетворення легко оборотні. З таким вейвлет-перетворенням тісно зв'язане так зване S-Перетворення. Якщо ми не хочемо, щоб при перетворенні Хаара границі значень послідовності подвоювалися (через підсумовування), треба брати напівсуму. Однак при цілому розподілі на 2 ми втрачаємо точність. Рішення даної проблеми виглядає так: нехай a і b - пари значень із вихідної послідовності. Тоді

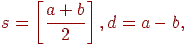
при цьому відновлення виглядає так:

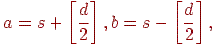
при цьому, якщо d - непарне, то при d > 0 до a додається 1, а якщо d < 0, то до b додається 1.

Лістинг 14.1. Алгоритм

В алгоритмі JPEG2000 [10] використовуються так звані вейвлеты Добеши (англ. Daubechies wavelet). У матричному виді для дії на вектор A довжини 8 дане перетворення задається так:

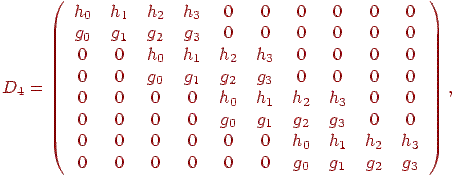
де

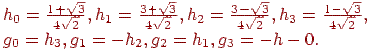
Як видно, матриця має розміри 8 × 10 через необхідність участі в підсумовуванні чотирьох компонентів. Т.е. насправді, така матриця множиться на наступний вектор:

A = (a₁a₂a₃a₄a₅a₆a₇a₈a₉a₁₀)^T .

Звичайно думають або a₉ = a₁, a₁₀ = a₂, або a₉ = a₈, a₁₀ = a₇. Використання вейвлет-перетворень при стиску зображень аналогічно використанню дискретний косинус-перетворення в алгоритмі JPEG, тобто саме перетворення - лише щабель конвеєра стиску.

Вейвлет-Перетворення мають дуже гарну частотно-просторову локалізацію й по цьому показнику перевершують традиційні косинус-перетворення й інші перетворення Фур'є. Таким чином, стає можливо застосовувати більше сильне квантування, поліпшуючи властивості послідовності для наступного стиску без втрат. Алгоритми стиску зображень, засновані на цьому перетворенні, при тім же ступені стиску показують кращі результати по збереженню якості зображення. До того ж обчислювальна складність дуже низька й становить O(N) (тут N - довжина послідовності, до якої застосовується перетворення). Однак поширеність форматів, що використовують стиск на основі вейвлет-перетворення, невелика через наявність патентів, а також через велику поширеність звичайного JPEG, що дає цілком прийнятні результати.