Фрактальное стиск
Фрактальное стиск ґрунтується на пошуку й кодуванні самоподібних областей у зображенні. При цьому використовуються системи итерируемых функцій (англ. IFS - Iterated Function System) [31], [12].
Визначення 14.6.1. Відображення 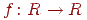 в повному метричному просторі
в повному метричному просторі 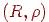 називається стискаючої, якщо
називається стискаючої, якщо 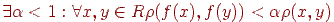 .
.
Cистеме зі 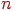 стискаючих відображень
стискаючих відображень 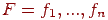 , що діють у повному метричному просторі
, що діють у повному метричному просторі 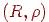 , ставиться у відповідність оператор системи итерируемых функцій
, ставиться у відповідність оператор системи итерируемых функцій
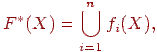
де 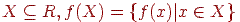 . Таке відображення є стискаючим з коефіцієнтом
. Таке відображення є стискаючим з коефіцієнтом
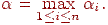
По теоремі про стискаючі відображення [3] існує нерухлива безліч 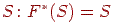 .
.

Рис. 14.7. Трикутник Серпинского
Розглянемо приклад дії системи итерируемых функцій. Нехай
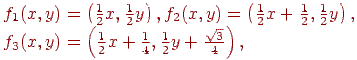
діють у просторі R = [0; 1]2 з евклідовою метрикою. Дані відображення є стискаючими 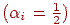 , і їхні нерухливі крапки є вершини рівностороннього трикутника (їхньої координати
, і їхні нерухливі крапки є вершини рівностороннього трикутника (їхньої координати 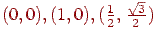 відповідно). Спочатку будемо послідовно застосовувати оператор F* даних перетворень до безлічі, обмеженій рівностороннім трикутником (наприклад, з координатами вершин, зазначеними вище). Нерухлива безліч S, одержуване при дії оператора даної системи итерируемых функцій, - це так званий трикутник Серпинского (див. мал. 14.7). Процес побудови трикутника Серпинского див. на мал. 14.8. Можна почати застосовувати оператор даних перетворень не до трикутника, а до квадрата. Нерухлива безліч буде таким же (див. мал. 14.9). Неважливо, з якої області починати (потрібно тільки компактність), - одержимо трикутник Серпинского.
відповідно). Спочатку будемо послідовно застосовувати оператор F* даних перетворень до безлічі, обмеженій рівностороннім трикутником (наприклад, з координатами вершин, зазначеними вище). Нерухлива безліч S, одержуване при дії оператора даної системи итерируемых функцій, - це так званий трикутник Серпинского (див. мал. 14.7). Процес побудови трикутника Серпинского див. на мал. 14.8. Можна почати застосовувати оператор даних перетворень не до трикутника, а до квадрата. Нерухлива безліч буде таким же (див. мал. 14.9). Неважливо, з якої області починати (потрібно тільки компактність), - одержимо трикутник Серпинского.
Іншим прикладом нерухливої безлічі S для оператора F* для деякої системи F із чотирьох аффинных перетворень є папороть Барнсли (див. мал. 14.10).

Рис. 14.8. Побудова трикутника Серпинского

Рис. 14.9. Побудова трикутника Серпинского із квадрата
Зображення папороті може займати (у гарному дозволі), а його опис за допомогою параметрів аффинных перетворення - кілька сотень байт! Відповідно, ідея стиску складається в пошуку таких систем перетворень, які б у процесі итерирования наближали бажане зображення. Завдання ставиться так:
по даній безлічі S знайти систему итерируемых функцій F так, що нерухлива безліч системи досить добре наближає S.
Складність такого завдання в загальному випадку дуже висока. Однак, якщо розглядати зображення як функцію (див. введення роздягнула 14.3) і обмежувати вид перетворень у такий спосіб:
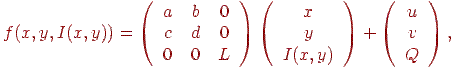
т.е. аффинными перетвореннями, то завдання спрощується. Проте час роботи, необхідне для пошуку коефіцієнтів перетворення, занадто велико. Для прискорення алгоритму пошуку коефіцієнтів накладають спеціальні обмеження на вид і розмір безлічей, до яких застосовуються перетворення, а також на сам вид перетворень, тобто фіксована безліч кутів повороту й коефіцієнтів масштабування. Таким чином, завдання стає дискретної й можливий прямий підбор параметрів.

Рис. 14.10. Папороть Барнсли
У реальному житті зображення, подібні до папороті Барнсли (тобто складаються тільки із самоподоб), зустрічаються рідко, тому очікувати схожого ступеня стиску не можна. Проте якість відновлених зображень при високих ступенях стиску значно перевершує JPEG. До недоліків алгоритму відносять дуже довгий час стиску в порівнянні з іншими методами, а також наявність патентів.
Дата добавления: 2015-04-03; просмотров: 1032;
