Розтяг і стиск.
1. Стержнями називають такі елементи конструкцій, довжина яких значно пере-вищує їх поперечні розміри. Якщо до кінців стержня прикладені дві однакові проти-лежно направлені сили, які діють вздовж його вісі, стержень розтягнутий (рис. 18а) або стиснутий (рис.18б).
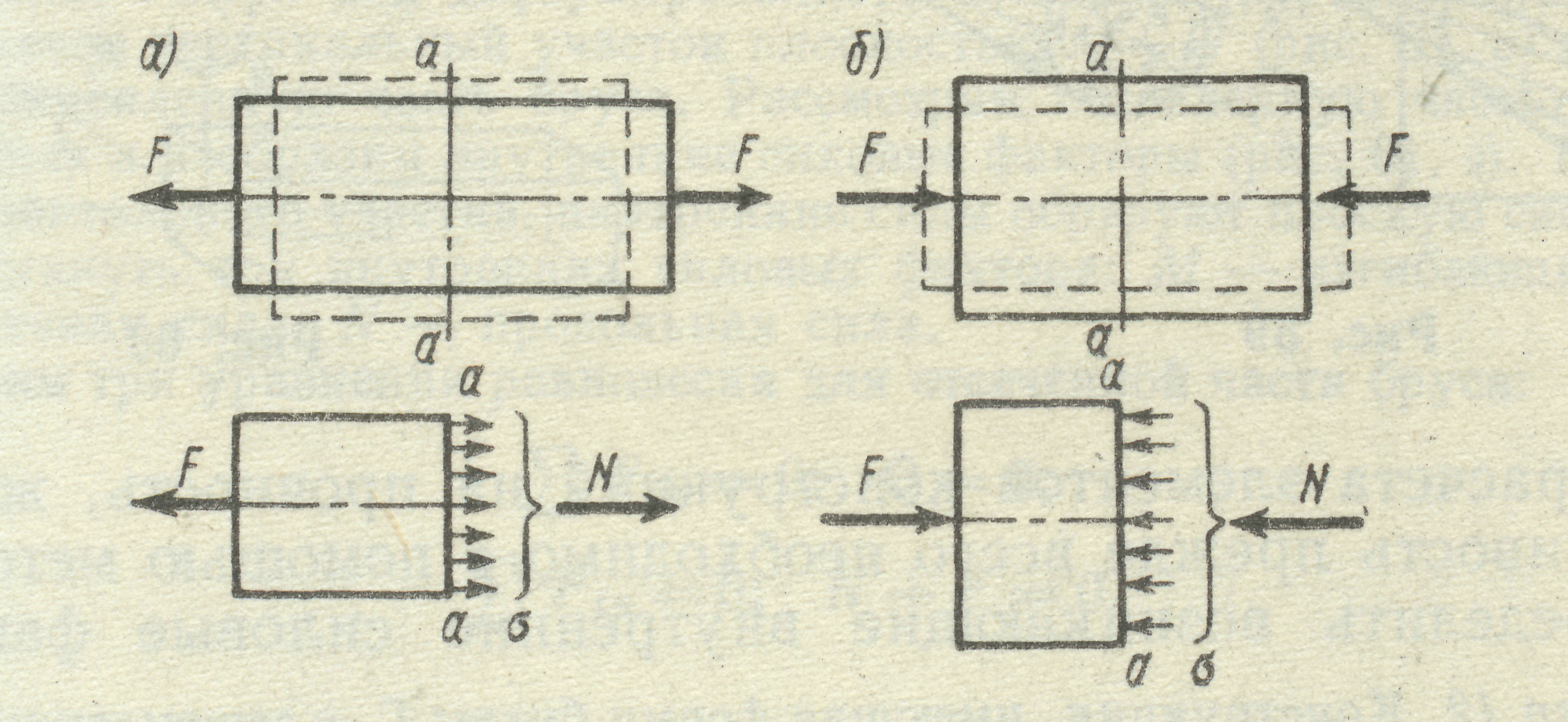
Рис. 18
При осьовому розтягу або стиску внутрішні сили в поперечному перерізі можуть бути замінені однією силою, направленою вздовж вісі - повздовжньою силою 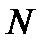 .
.
Зсув виникає в тому випадку, коли в поперечному перерізі балки внутрішні сили приводяться до однієї сили, розміщеної в площині перерізу - поперечній силі 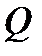 .
.
При крученні виникає один внутрішній фактор - обертовий момент 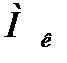
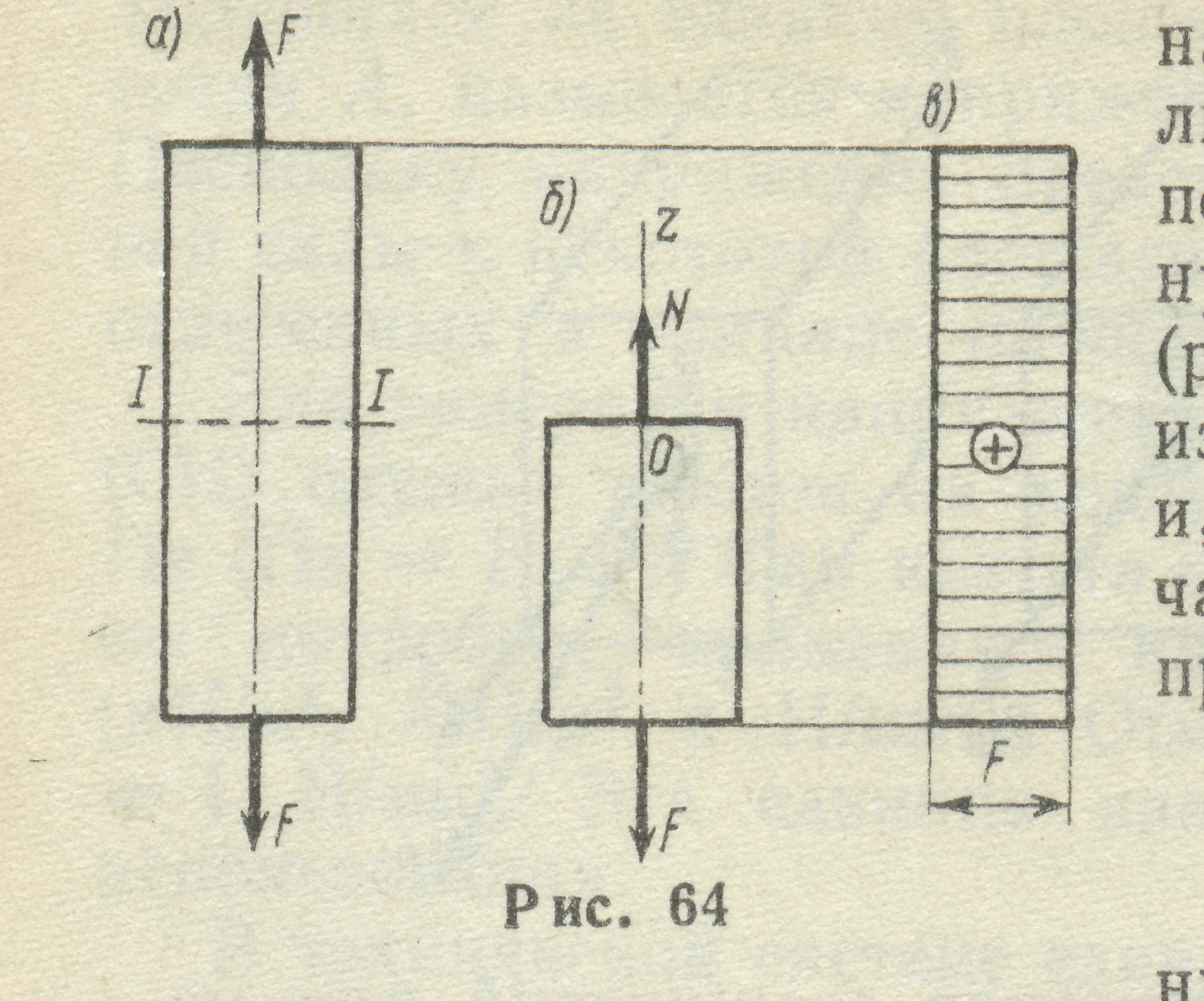 2. Якщо до кінців стержня прикладені дві однакові протилежно направлені сили , які діють вздовж його осі, стержень розтягнутий або стиснутий. Переріжемо стержень довільним перерізом
2. Якщо до кінців стержня прикладені дві однакові протилежно направлені сили , які діють вздовж його осі, стержень розтягнутий або стиснутий. Переріжемо стержень довільним перерізом  та розглядаючи рівновагу нижньої частини (рис. 19), знайдемо величину повздовж-ньої сили:
та розглядаючи рівновагу нижньої частини (рис. 19), знайдемо величину повздовж-ньої сили:
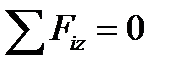 ;
; 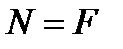 .
.
У випадку розтягування стержня повздовжню силу 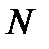 вважаємо додатною, при стиску - від’єм-ною.
вважаємо додатною, при стиску - від’єм-ною.
Діаграма зміни повздовжньої сили по довжині Рис. 19 стержня називається епюром повздовжніх сил.
3. При розтягу або стиску осьовими силами стержнів з однорідного матеріалу по-перечні перерізи, достатньо віддалені від точок прикладання зовнішніх сил, залиша-ються плоскими та переміщуються поступально в напрямку деформації. Ці напруги перпендикулярні до поперечного перерізу, отже є нормальними, їх знаходять шля-хом ділення повздовжньої сили N на площу А
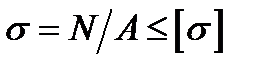 .
.
4. Під час розтягу стержень змінює свої геометричні розміри. Відношення видов-ження до початкової довжини стержня називається повздовжньою деформацією.
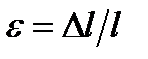 .
.
Відношення зміни поперечного перерізу до попереднього розміру називають попе-речною деформацією.
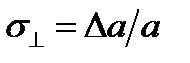 .
.
Відношення поперечної деформації до повздовжньої, при пружному розтягу (стис-ку) для даного матеріалу називається коефіцієнтом поперечної деформації або коефі-цієнтом Пуассона.
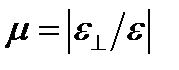 .
.
5. Повздовжня деформація прямо пропорційна відповідній нормальній напрузі
(Закон Гука):
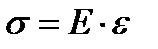 або
або 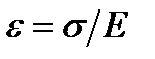 .
.
6. Величина Е, яка характеризує жорсткість матеріалу, тобто здатність матеріалу опиратись пружній деформації називається модулем повздовжньої пружності.(Н/м, Н/мм ).
7.Випробування матеріалів на розтяг і стиск поділяються по характеру приклада-ння зовнішніх сил: статичні, динамічні (випробування ударним навантаженням) та випробування на витривалість (навантаженням, яке викликає напруги, які змінюють-ся з часом).
8. Основні механічні характеристики:
 межа пружності;
межа пружності;
 межа міцності;
межа міцності;
 межа текучості.
межа текучості.
9. На основі експериментально знайдених меж напруг призначають допустимі напруги:
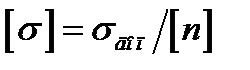 .
.
 Для пластичних матеріалів межа текучості:
Для пластичних матеріалів межа текучості:
 .
.
 Для крихких матеріалів межа міцності:
Для крихких матеріалів межа міцності:
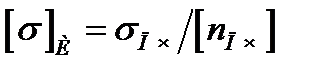 .
.
10. Міцність стержня при осьовому розтягу або стиску забезпечена, якщо для кожного його поперечного перерізу найбільше (робоче) напруження не перевищує допустимого:
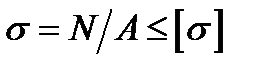 .
.
Під час розрахунків вирішуються такі задачі:
 перевірка міцності;
перевірка міцності;
 підбір перерізу;
підбір перерізу;
 визначення допустимої повздовжньої сили.
визначення допустимої повздовжньої сили.
Згин.
1. Елементи конструкцій, які працюють на згин, називають балками.
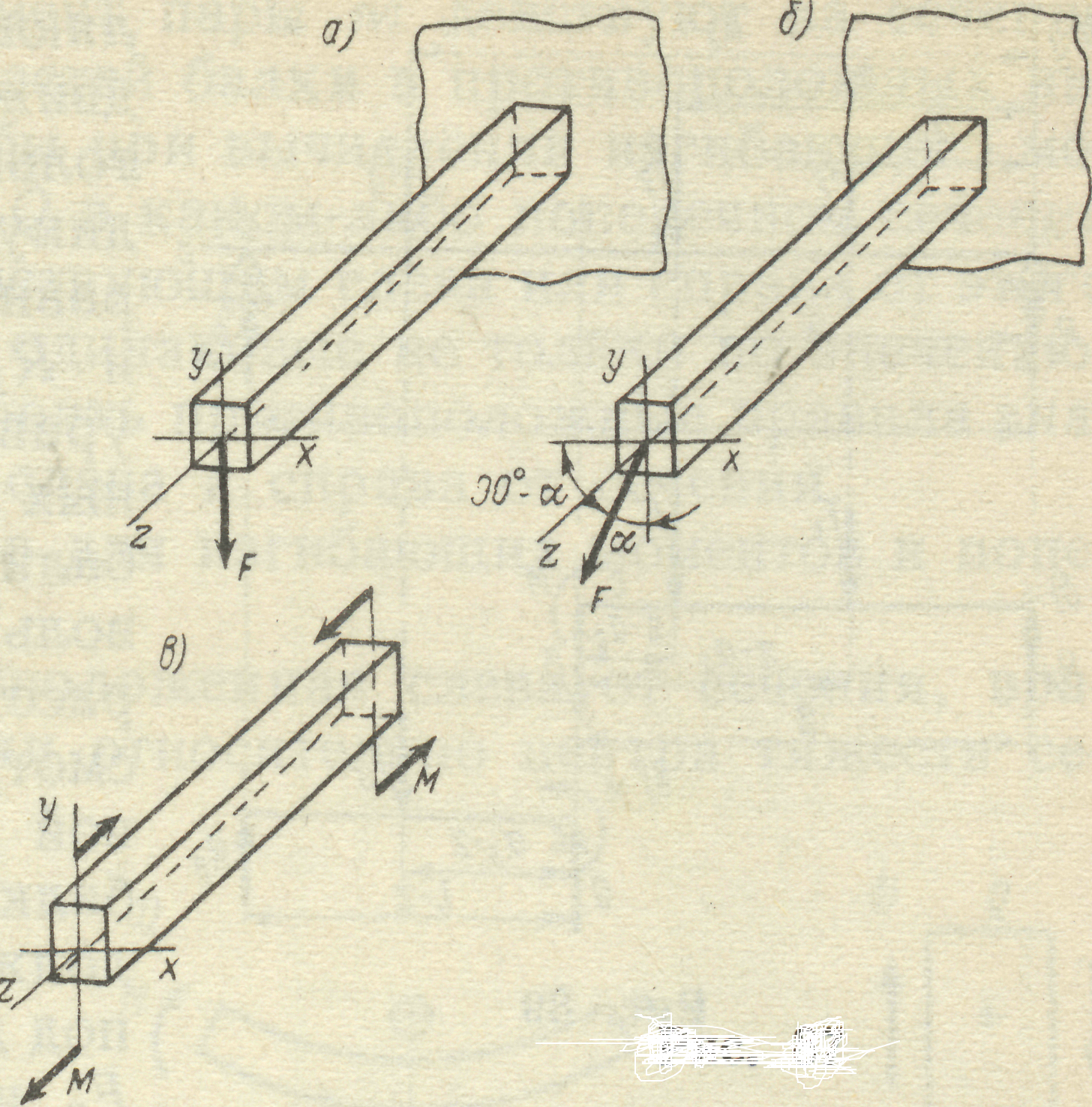 2. Найчастіше зустрічається прямий згин (рис. 20а), коли зовнішні сили, перпенди-кулярні до повздовжньої вісі балки, діють в пло-щині, яка проходить через вісь балки та одну з головних центральних осей її поперечного пере-різу.
2. Найчастіше зустрічається прямий згин (рис. 20а), коли зовнішні сили, перпенди-кулярні до повздовжньої вісі балки, діють в пло-щині, яка проходить через вісь балки та одну з головних центральних осей її поперечного пере-різу.
Якщо сили, які викликають деформацію зги-ну, діють в площині, яка проходить через вісь балки, але не проходить через одну з головних центральних осей її поперечного перерізу, має місце косий згин (рис. 20 б)
В поперечних перерізах балок при згині вини-кають два внутрішні силові фактори: згинаючий момент та поперечна сила. Однак у випадку, коли поперечних перерізах балки виникає тіль- Рис. 20 ки один фактор - згинаючий момент, а попереч-
на сила дорівнює нулю. У даному випадку згин називають чистим (рис. 20 в).
3. Поперечна сила та згинаючий момент в будь-якому поперечному перерізі балки визначаються за відомими зовнішніми силами, які діють на балку (рис. 21).
 Проведемо умовно довільний переріз С на відстані
Проведемо умовно довільний переріз С на відстані 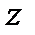 від лівої опори та роз-глянемо умови рівноваги правої та лівої частини балки. Ліва частина повинна бути в рівновазі під дією зовнішніх сил
від лівої опори та роз-глянемо умови рівноваги правої та лівої частини балки. Ліва частина повинна бути в рівновазі під дією зовнішніх сил  ,
, 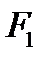 ,
, 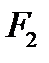 ; права під дією
; права під дією 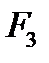 та
та 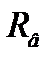 .
.
Внутрішні сили в будь-якому перері-зі замінимо поперечною силою 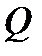 та згинаючим моментом
та згинаючим моментом 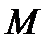 .
.
Умова рівноваги для сил,які діють в лівій частині матиме вигляд:
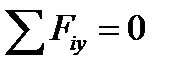 ;
; 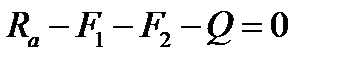 ;
;
Рис. 21 Рівняння моментів відносно точки С:
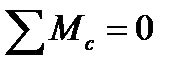 ;
; 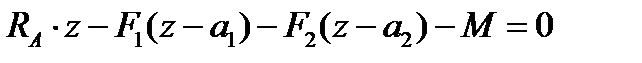 .
.
Розв’язавши перше з рівнянь відносно 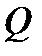 , а друге відносно
, а друге відносно 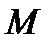 , отримаємо:
, отримаємо:
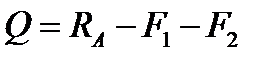 ;
;
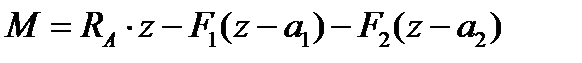 .
.
Поперечна сила в будь-якому поперечному перерізі балки чисельно дорівнює алгебраїчній сумі проекцій на вісь 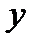 у зовнішніх сил, діючих на балку по одну сторону від перерізу, який розглядається, а згинаючий момент - алгебраїчній сумі моментів сил взятих відносно центра тяжіння перерізу.
у зовнішніх сил, діючих на балку по одну сторону від перерізу, який розглядається, а згинаючий момент - алгебраїчній сумі моментів сил взятих відносно центра тяжіння перерізу.
Внутрішні силові фактори в перерізах балок - поперечна сила 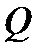 та згинаючий момент
та згинаючий момент 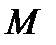 - залежать від зовнішнього навантаження та змінюються по довжині балки.
- залежать від зовнішнього навантаження та змінюються по довжині балки.
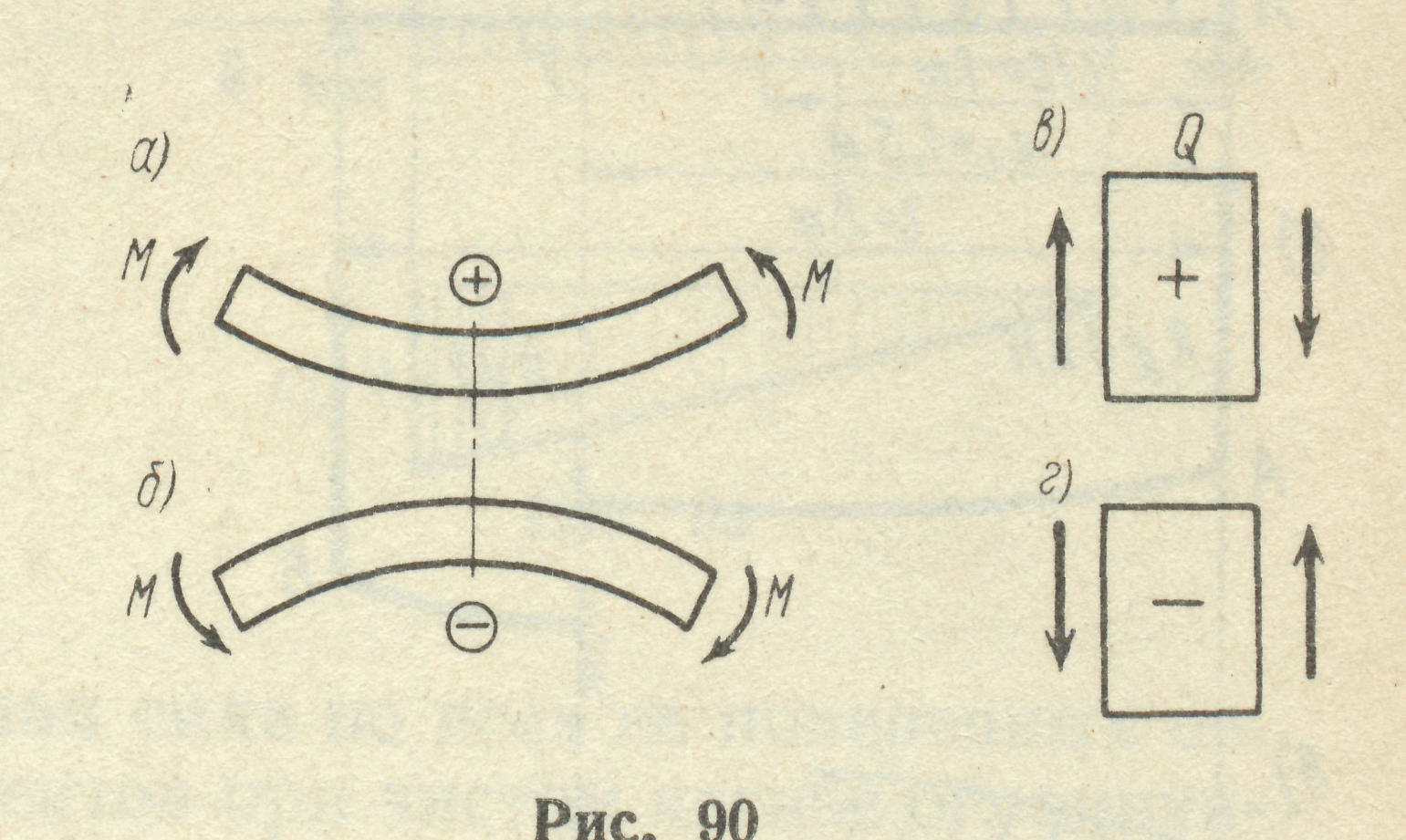 Якщо зовнішня сила , яка розміщена зліва від перерізу, обертає залишену частину балки віднос-но центра перерізу за ходом годинникової стрілки, згинаючий момент вважають додатним (рис. 22а), якщо проти - від’ємним (рис. 22б).
Якщо зовнішня сила , яка розміщена зліва від перерізу, обертає залишену частину балки віднос-но центра перерізу за ходом годинникової стрілки, згинаючий момент вважають додатним (рис. 22а), якщо проти - від’ємним (рис. 22б).
Якщо зовнішні сили діють зліва від перерізу вгору , а справа від перерізу - вниз, поперечна сила додатна (рис.22в). При зворотній дії сил поперечна
Рис. 22 сила від’ємна (рис. 22г).
4. Між навантаженням та епюрами поперечних сил і моментів існує взаємозв’язок (рис. 23):
v на ділянках, де згинаючий момент постійний(чистий згин), поперечна сила дорів-нює нулю;
v на ділянках, вільних від завантаження рівномірно розподіленим навантаженням: поперечна сила постійна, а згинаючий момент змінюється за лінійним законом (пряма лінія);
v на ділянках, завантажених рівномірно розподіленим навантаженням: поперечна сила змінюється за лінійним законом, а згинаючий момент по параболі.
v в точках, де поперечна сила дорівнює нулю ( 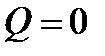 ), значення моменту приймає максимальне, або мінімальне значення.
), значення моменту приймає максимальне, або мінімальне значення.
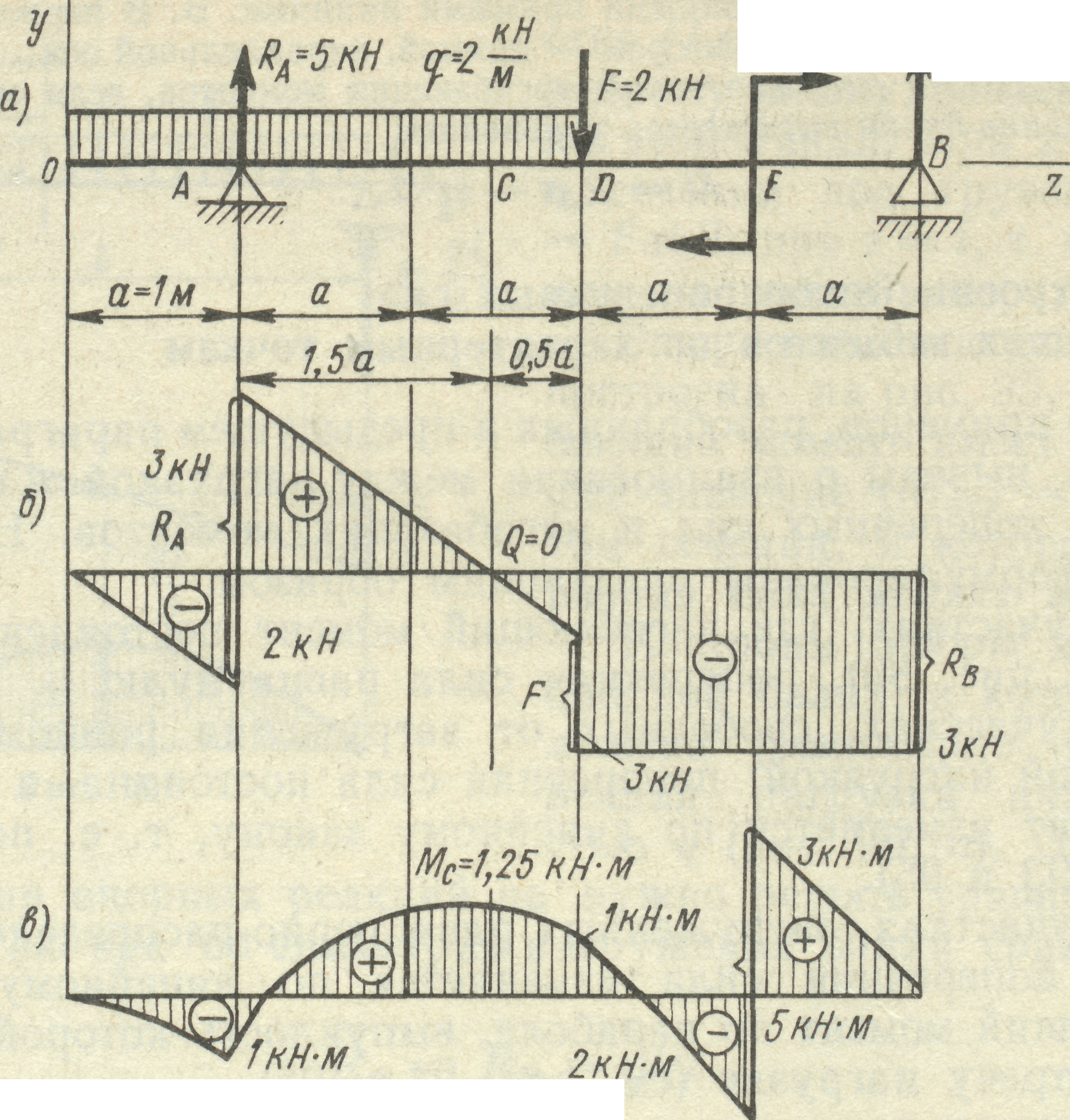
Рис. 23
5. Відношення осьового моменту інерції до найбільш віддалених волокон симет-ричного перерізу називають осьовим моментом опору:
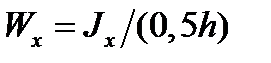 .
.
За абсолютним значенням нормальне напруження в симетричному перерізі можна визначити за формулою:
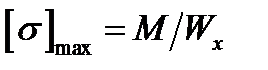 .
.
6. За допомогою умови міцності за нормальним напруженням при згині можна вирішувати такі задачі:
 перевірка міцності (проводиться у випадку, коли відомі розміри перерізу балки, найбільший згинаючий момент та допустиме напруження);
перевірка міцності (проводиться у випадку, коли відомі розміри перерізу балки, найбільший згинаючий момент та допустиме напруження);
 підбір перерізу (проводиться у випадку, коли задані навантаження, які діють на балку, тобто можна визначити найбільший згинаючий момент та допустиме напруження);
підбір перерізу (проводиться у випадку, коли задані навантаження, які діють на балку, тобто можна визначити найбільший згинаючий момент та допустиме напруження);
 визначення найбільшого допустимого згинаючого моменту (проводиться у випадку, якщо задані розміри перерізу балки та допустиме напруження).
визначення найбільшого допустимого згинаючого моменту (проводиться у випадку, якщо задані розміри перерізу балки та допустиме напруження).
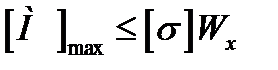 .
.
Дата добавления: 2015-04-03; просмотров: 7084;
