Плоска система збіжних сил.

1.Сили називають збіжними, якщо їх лінії дії перетинаються в одній точці. Розріз-няють плоску та просторову систему збіжних сил.

2. За третьою аксіомою статики силу можна перенести вздовж лінії її дії, тому збіжні сили можна завжди перенести в одну точку та побудувати силовий багато-кутник (рис. 5).

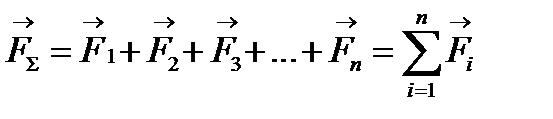
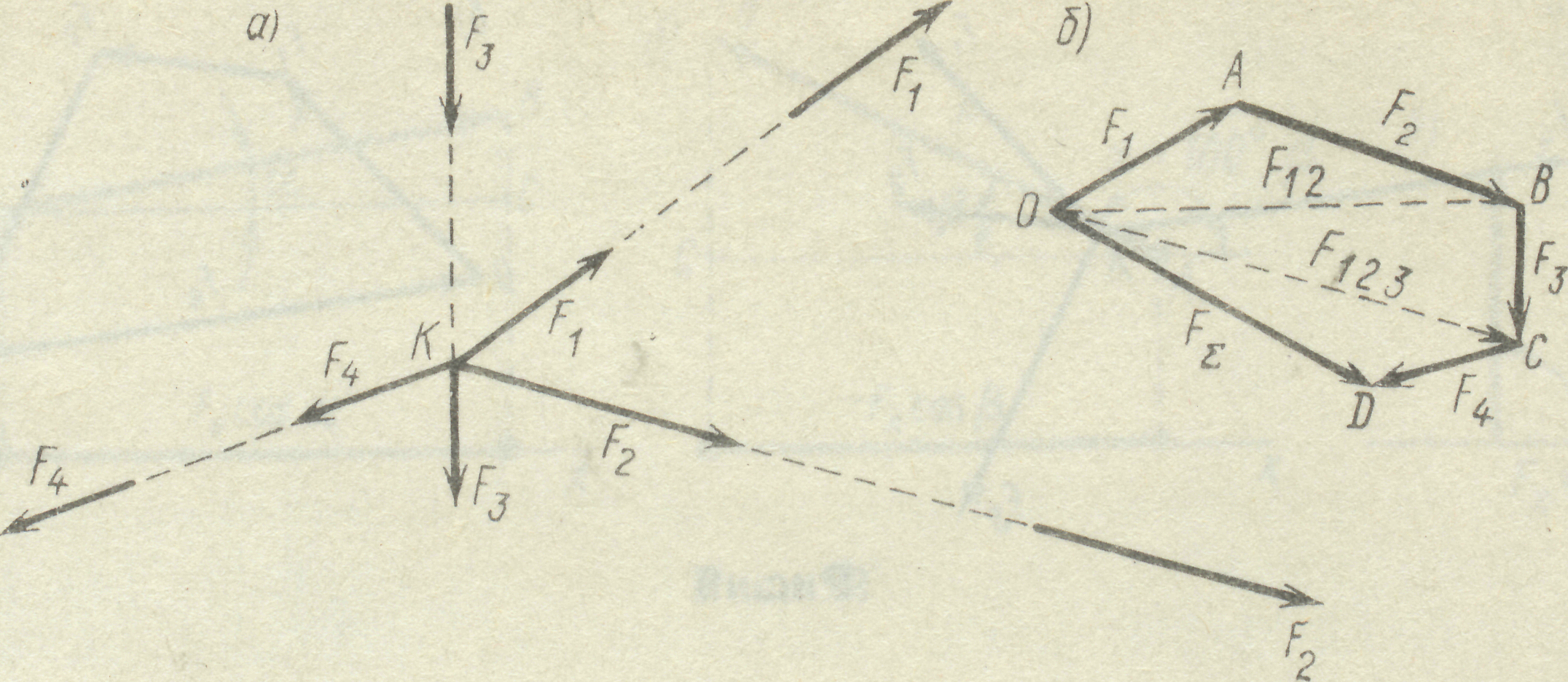
Рис. 5

Якщо при побудові силового багатокутника кінець останньої сили співпаде з по-чатком першої, то рівнодіюча 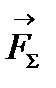системи дорівнює нулю. Така система збіжних сил знаходиться в стані рівноваги.

3.Віссю називають пряму лінію, для якої визначено відповідний напрям.

Проекція вектора на вісь є скалярною величиною, яка обмежена відрізком вісі утвореним перпендикулярами, опу-щеними на неї з кінців вектора.

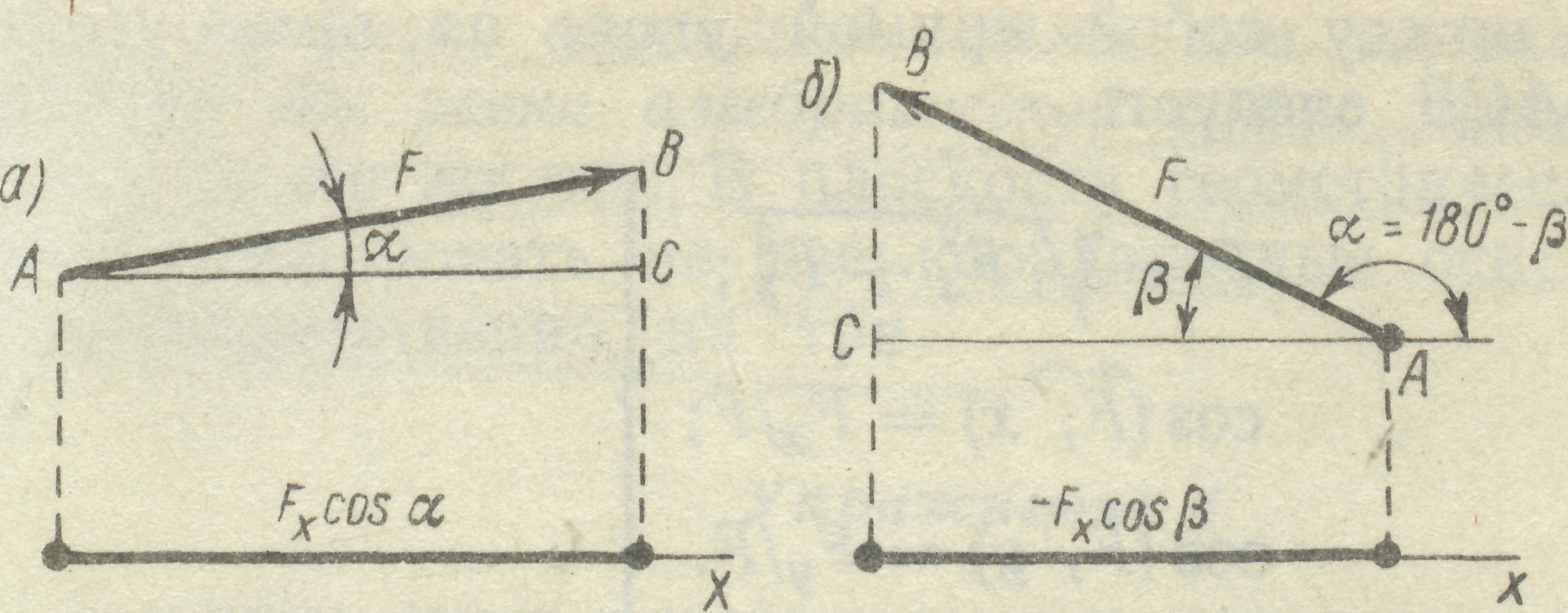
Проекція вважається додатною, якщо напрямок від початку проекції до її кінця співпадає з позитивним напрямком вісі. Проекція вважається від`ємною, якщо напрямок від почат-ку проекції до її кінця протилежний Рис. 6 додатному напрямку вісі.

3.1. У випадку, коли вектор сили 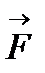становить з додатним напрямом вісі 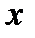гострий кут 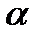(рис. 6 а), щоб знайти проекцію необхідно з початку та кінця вектора сили опустити перпендикуляри на вісь 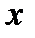; отримаємо:

.

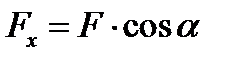Проекція в даному випадку додатна.

3.2. Якщо сила 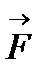складає з позитивним напрямом вісі 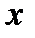тупий кут 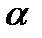(рис.6 б), то 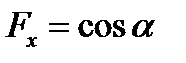, але оскільки ;

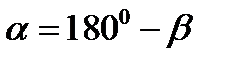отримаємо:

.

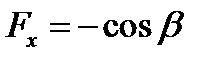Проекція в даному випадку від’ємна.

3.3. У випадку, коли сила 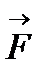перпендикулярна до осі 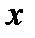, проекція сили 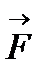на вісь 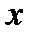дорівнює нулю:

.

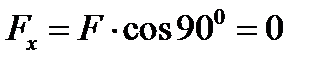Проекція сили на вісь координат дорівнює добутку модуля сили на косинус кута між вектором сили та позитивним напрямком вісі/

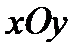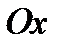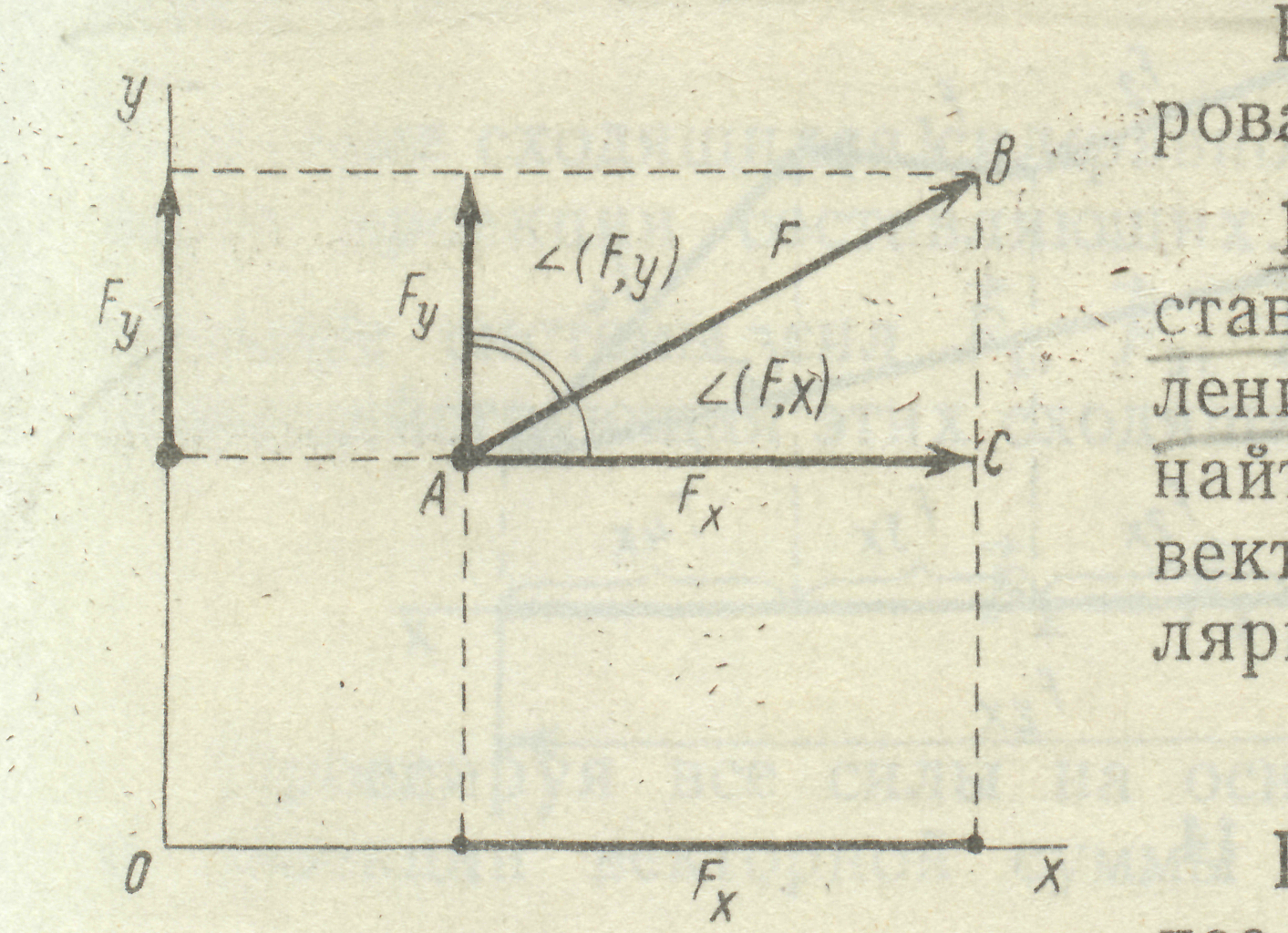
4.Силу, розміщену на площині можна спроектувати на дві координатні вісі та 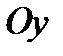(рис.7). Оскільки проекції утворюють між собою прямий кут, з прямокутного трикутника АВС маємо:

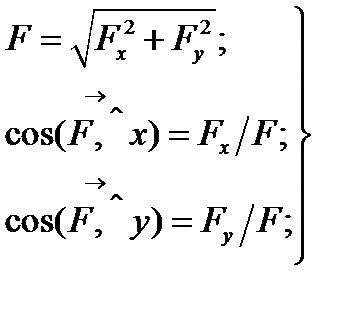
Даними формулами користуються для визначе-ння модуля та напрямку сили, якщо відомі її про-

Рис. 7 екції на вісі координат.

5. Проекція векторної суми або рівнодіючої на будь-яку вісь дорівнює алгебраїч-ній сумі проекцій векторів, які додаються, на ту саму вісь (рис. 8).

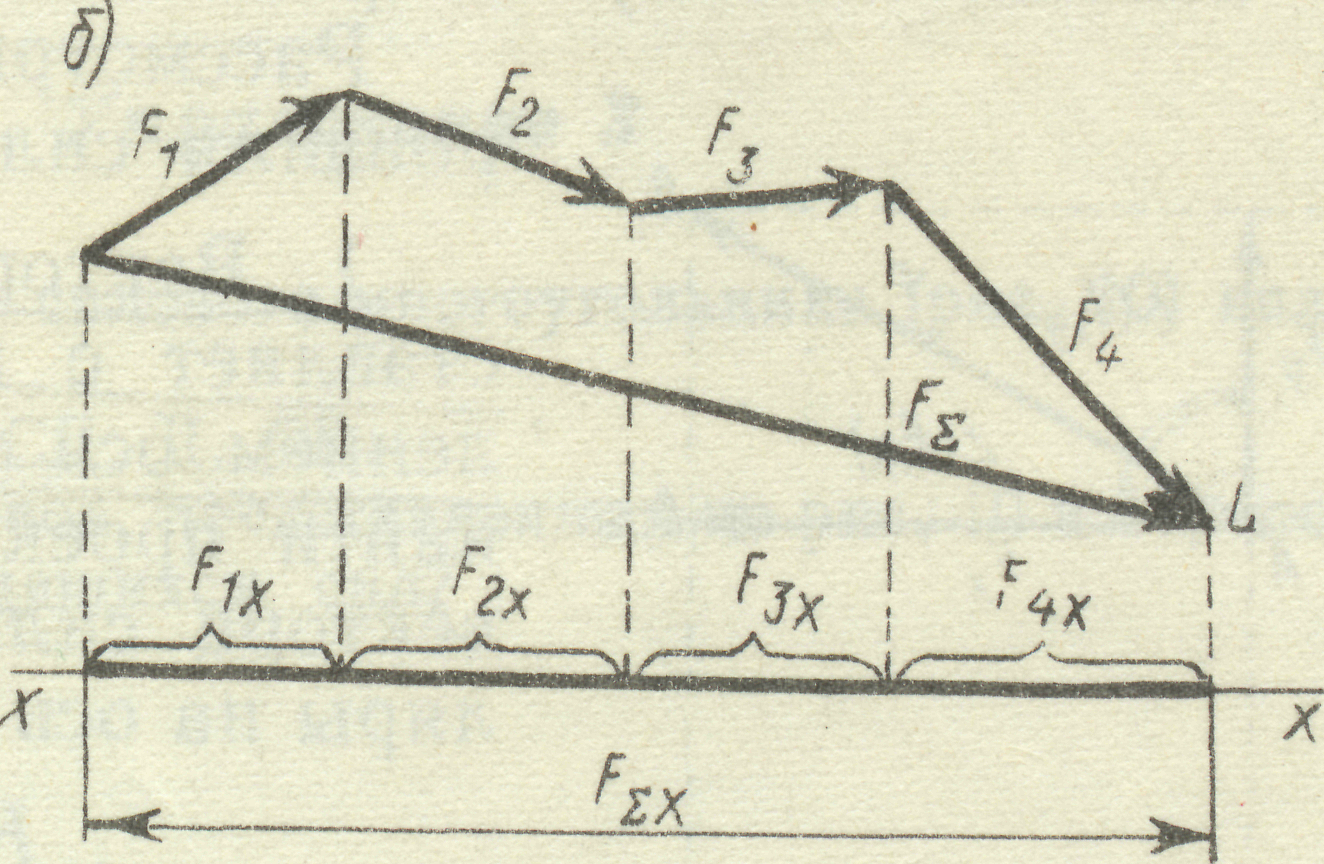
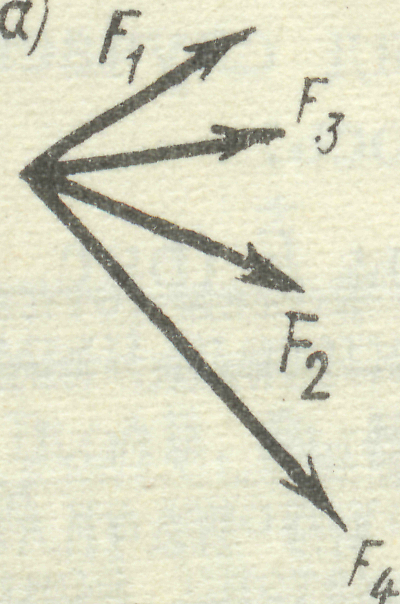
Рис. 8

5.Система збіжних сил знаходиться в стані рівноваги, якщо алгебраїчна сума проекцій її доданків на кожну з двох координатних осей дорівнюють нулю.

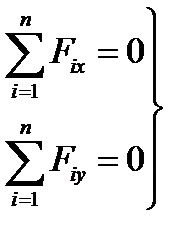Рівняння рівноваги плоскої системи збіжних сил.

Для спрощення запису рівнянь можна опускати індекси та суми.