Довільно плоска система сил.
1 Момент сили 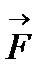 відносно точки О визначається добутком модуля сили на дов-жину перпендикуляра, опущеного з точки на лінію дії сили.
відносно точки О визначається добутком модуля сили на дов-жину перпендикуляра, опущеного з точки на лінію дії сили.
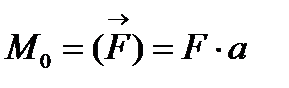
При закріпленні тіла в точці О сила 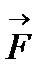 намагається повернути тіло навколо цієї точки. Точка О, відносно якої береться момент, називається центром моменту, а довжина перпендикуляра
намагається повернути тіло навколо цієї точки. Точка О, відносно якої береться момент, називається центром моменту, а довжина перпендикуляра 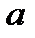 - плечем моменту.
- плечем моменту.
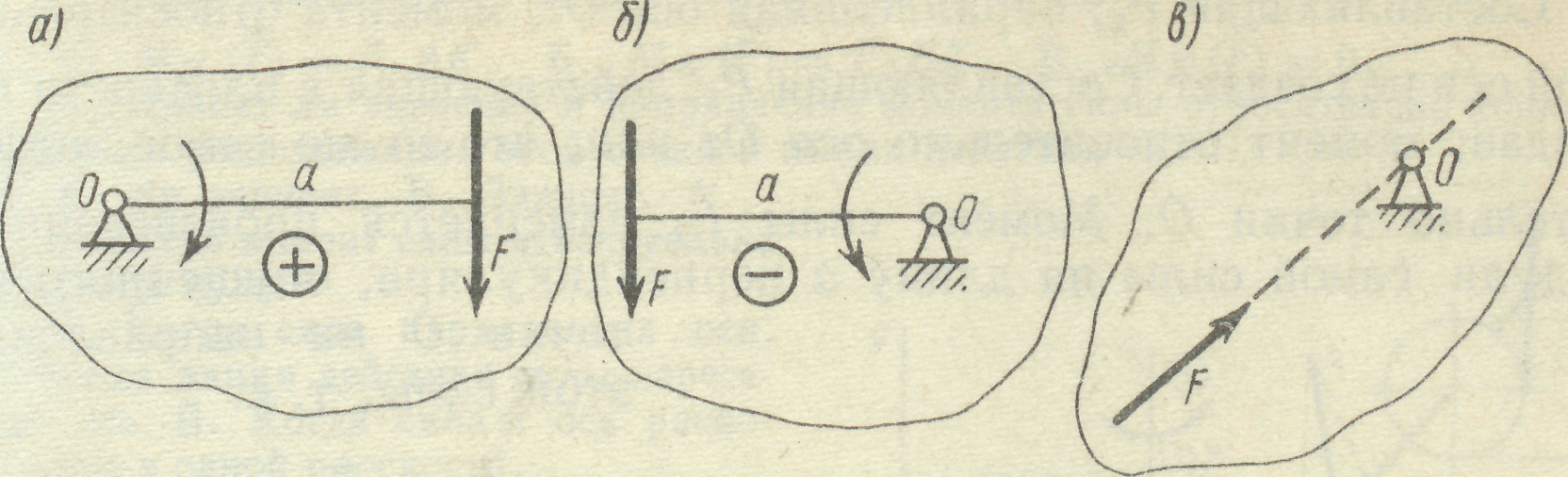
Рис 9
Момент прийнято вважати додатним, якщо сила намагається обертати тіло за годинниковою стрілкою (рис. 9а), а від’ємним, якщо проти годинникової стрілки (рис. 9 б). У випадку коли лінія дії сили проходить через дану точку, момент сили дорівнює нулю (рис. 9в).
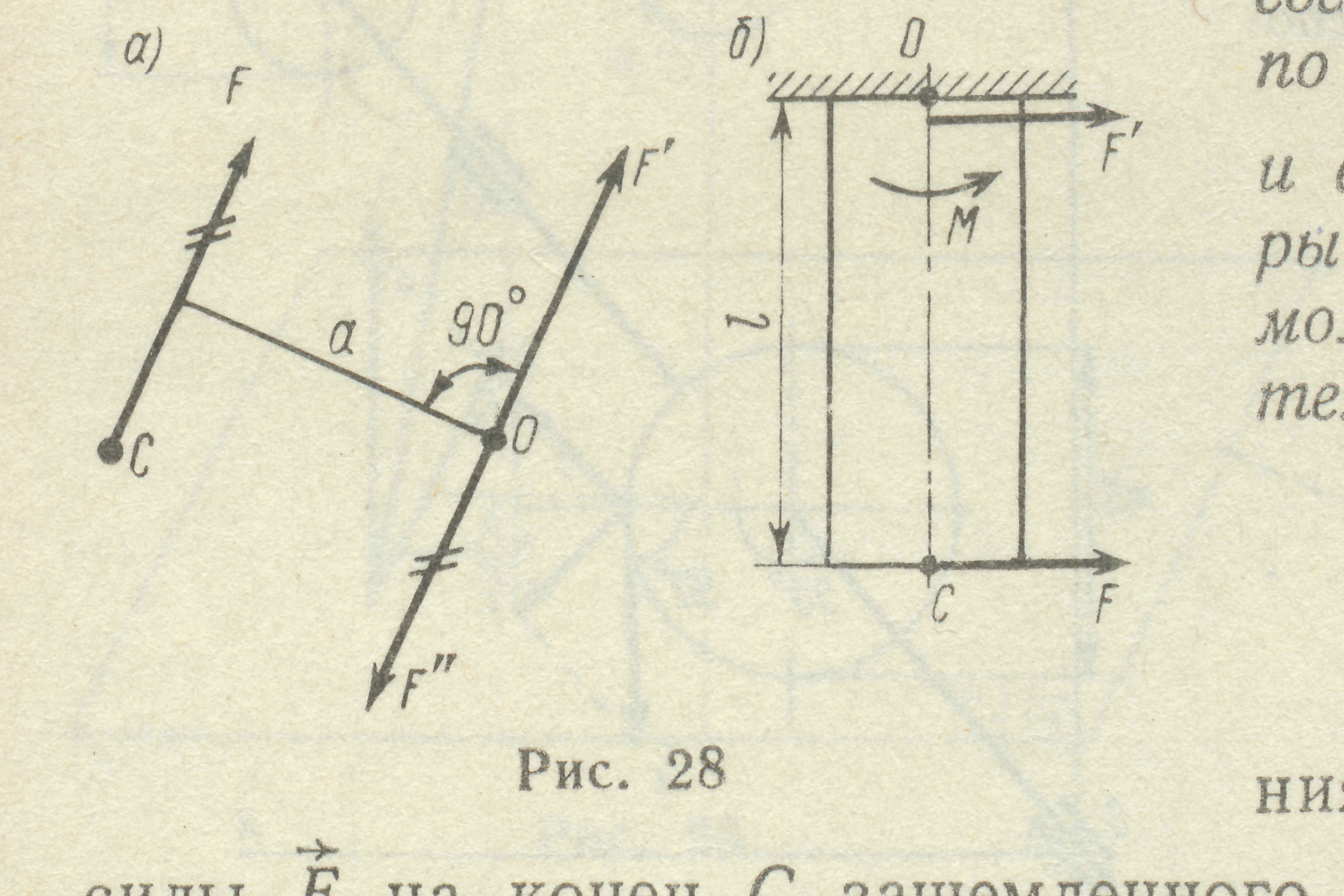 2. При приведенні сили
2. При приведенні сили 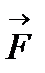 до довільної точки, яка не ле-жить на лінії дії сили, отримується еквівалентна система, яка складається з сили, такої самої за модулем та напрям-ком, як і сила
до довільної точки, яка не ле-жить на лінії дії сили, отримується еквівалентна система, яка складається з сили, такої самої за модулем та напрям-ком, як і сила 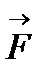 , та приєднаної пари сил, момент якої дорівнює моменту даної сили відносно точки приведення (рис. 10):
, та приєднаної пари сил, момент якої дорівнює моменту даної сили відносно точки приведення (рис. 10):
Рис. 10 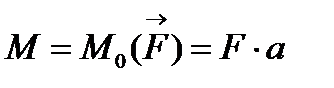 .
.
3. Плоска система сил в результаті приведення до даної точки О (рис. 11) заміню-ється еквівалентною їй системою, яка складається з однієї сили (головного вектора) та однієї пари (головного моменту).
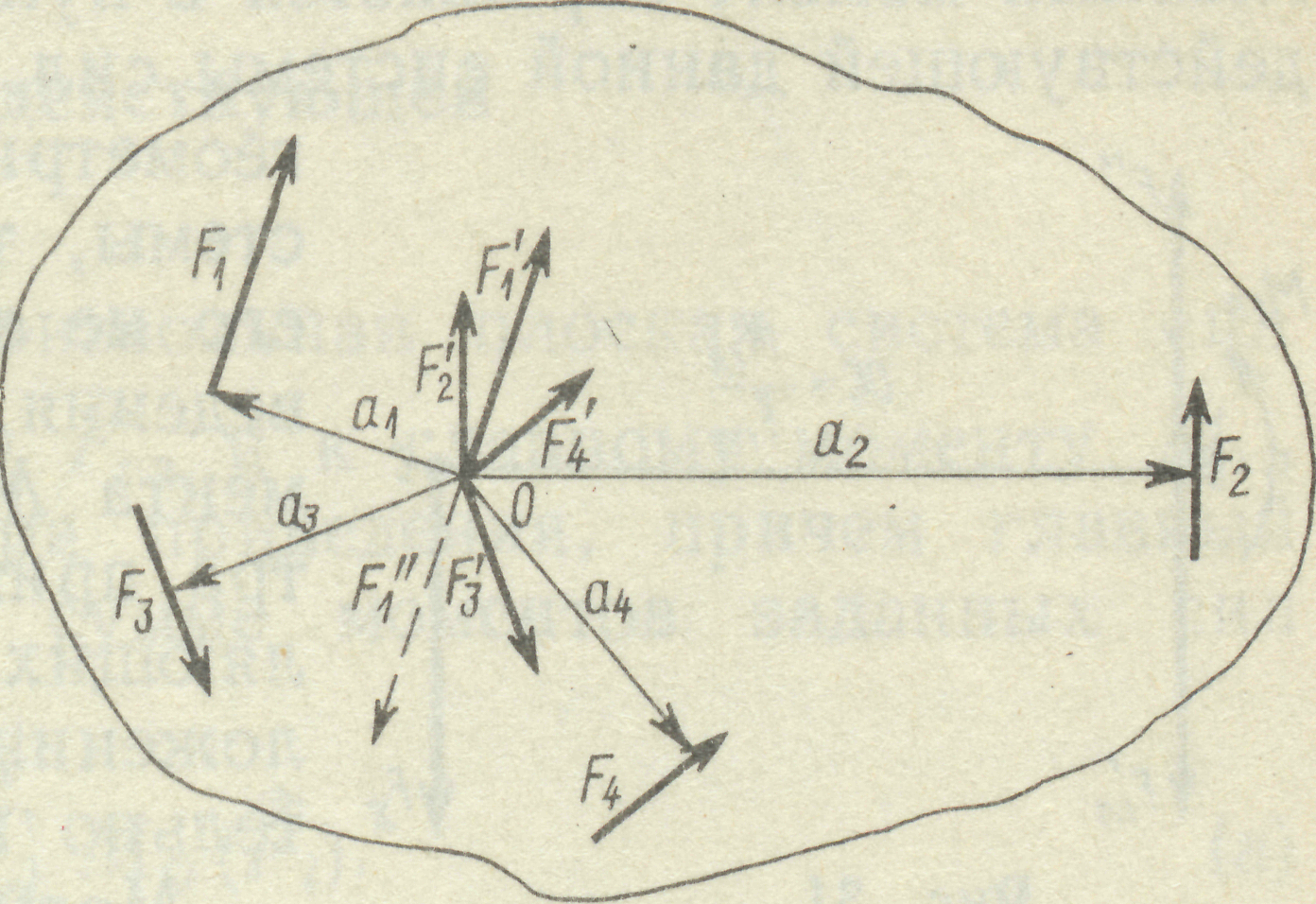
Рис. 11
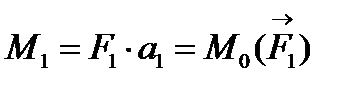 ;
; 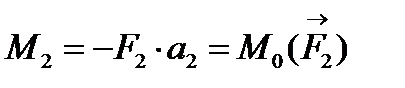 ;
;
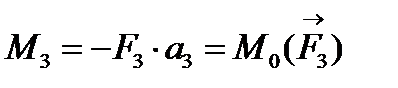 ;
; 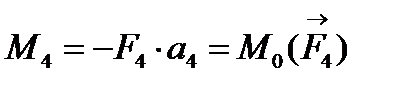 .
.
4. Сили, що збігаються в точці О можна замінити однією силою 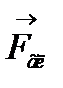 , яка дорівнює геометричній сумі складових:
, яка дорівнює геометричній сумі складових:
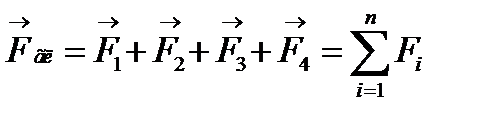 .
.
 Силу , яка дорівнює геометричній сумі заданих сил, називають головним вектором системи.
Силу , яка дорівнює геометричній сумі заданих сил, називають головним вектором системи.
 Момент, який дорівнює алгебраїчній сумі моментів заданих сил відносно точки О називається головним моментом:
Момент, який дорівнює алгебраїчній сумі моментів заданих сил відносно точки О називається головним моментом:
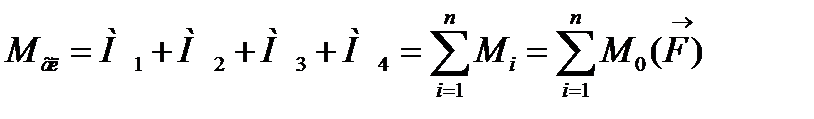
5. Теорема Варіньона: Момент рівнодіючої плоскої системи сил відносно довільно взятої точки дорівнює алгебраїчній сумі моментів складових сил відносно тієї ж точки:
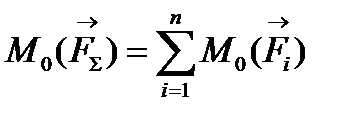 .
.
6. Для рівноваги системи сил, довільно розміщених на площині, необхідно і доста-тньо, щоб головний вектор та головний момент цих сил відносно будь-якого центра кожний дорівнював нулю:
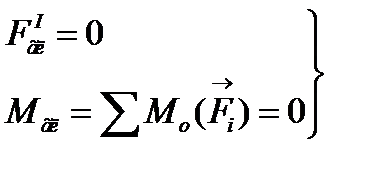
7. Балки (балочні системи) тіла видовженої форми призначені для сприйняття поперечних навантажень.
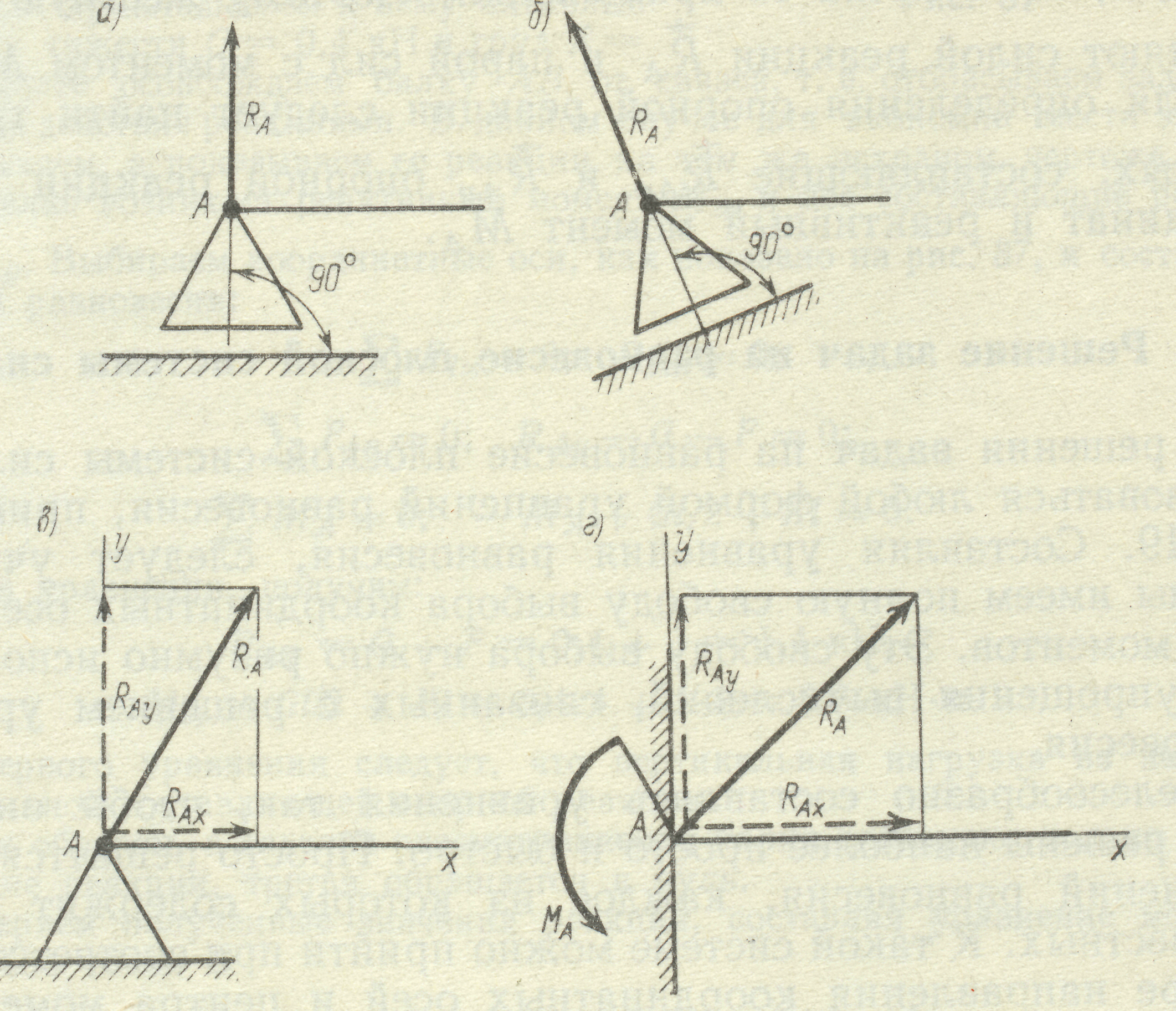
Рис. 12
 Шарнірно-рухома опора (рис. 12а, б) (допускає поворот навколо вісі шарніра та лінійне переміщення паралельно опорної площини).
Шарнірно-рухома опора (рис. 12а, б) (допускає поворот навколо вісі шарніра та лінійне переміщення паралельно опорної площини).
 Шарнірно нерухома опора (рис. 12в) (допускає поворот тільки навколо вісі шарніра).
Шарнірно нерухома опора (рис. 12в) (допускає поворот тільки навколо вісі шарніра).
 Жорстке защемлення (рис. 12г) (не допускає ніяких лінійних переміщень та поворотів).
Жорстке защемлення (рис. 12г) (не допускає ніяких лінійних переміщень та поворотів).
Для рішення задач на рівновагу плоскої системи сил можна користуватись будь-якою формулою рівноваги. В якості моментів рекомендують вибирати точку, де перетинаються дві невідомі сили; рівняння моментів відносно цієї точки матиме одне невідоме. Напрямок координатних осей 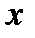 та
та 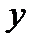 необхідно вибирати таким чином, щоб вісі були перпендикулярні деяким невідомим силам (при складанні рів-нянь проекцій невідомі, перпендикулярні відповідній вісі, в ці рівняння не ввійдуть.
необхідно вибирати таким чином, щоб вісі були перпендикулярні деяким невідомим силам (при складанні рів-нянь проекцій невідомі, перпендикулярні відповідній вісі, в ці рівняння не ввійдуть.
Центр ваги. Геометричні характеристики плоских перерізів.
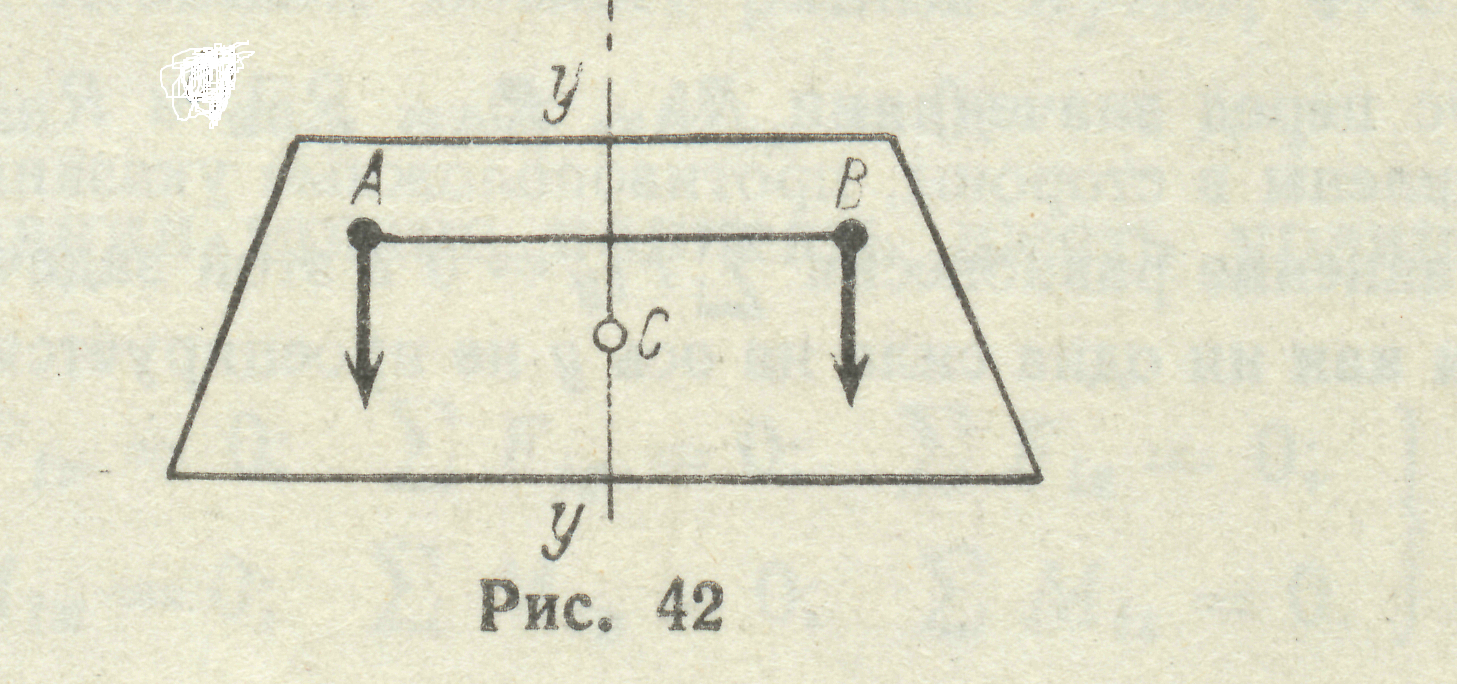 1.Якщо на тіло діють дві паралельні сили, то рівнодіюча цих сил дорівнює їх сумі, паралельна до них, напрямлена в ту ж сторону, а її лінія дії ділить плече на частини обернено пропорційні цим силам (рис. 13).
1.Якщо на тіло діють дві паралельні сили, то рівнодіюча цих сил дорівнює їх сумі, паралельна до них, напрямлена в ту ж сторону, а її лінія дії ділить плече на частини обернено пропорційні цим силам (рис. 13).
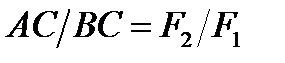 .
.
Точка С називається центром паралельних сил, її по-ложення не залежить від напрямку сил, які додаються. Будь-яке тло можна розглядати, як складене з великої кількості малих частинок, на які діють сили тяжіння.
Рис. 13 Рівнодіючу цих сил називають силою тяжіння.
2. Центр паралельних сил тяжіння, діючих на всі частинки тіла, називають цент-ром тяжіння тіла. Центр тяжіння тіла не змінює свого розташування при повороті тіла
3.Положення (координати) центра просторової системи паралельних сил визнача-ють за формулами:
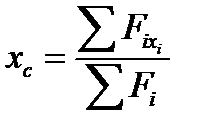 ;
; 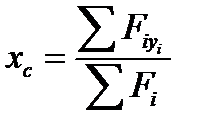 ;
; 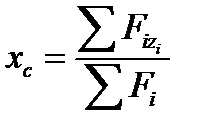 .
.
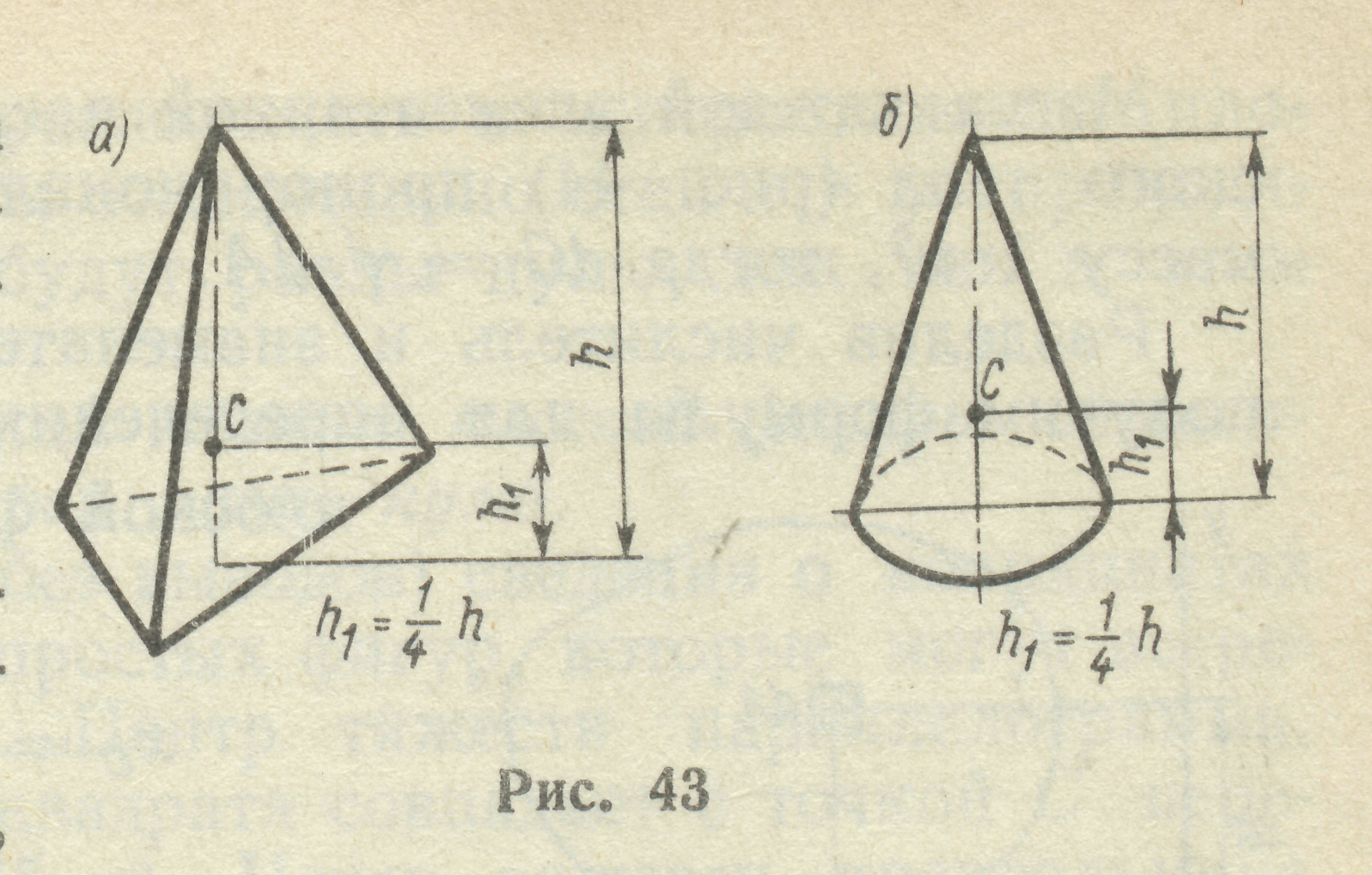 4.Центр ваги симетричного тіла завжди лежить в площі симетрії. Площа симетрії поділяє тіло таким чином, що кожній матеріальній точці, яка знаходиться по одну сторону площини, відповідає однакова за масою точка по іншу сторону площини, причому лінія, яка з’єднує ці точки, перпендикулярна до площини симетрії та ділиться нею пополам. Центр ваги плоскої симетричної фігури лежить на вісі симетрії (рис. 14).
4.Центр ваги симетричного тіла завжди лежить в площі симетрії. Площа симетрії поділяє тіло таким чином, що кожній матеріальній точці, яка знаходиться по одну сторону площини, відповідає однакова за масою точка по іншу сторону площини, причому лінія, яка з’єднує ці точки, перпендикулярна до площини симетрії та ділиться нею пополам. Центр ваги плоскої симетричної фігури лежить на вісі симетрії (рис. 14).
Для плоских тіл центр тяжіння визначають Рис. 14 тільки двома координатами, а об’ємних - трьома:
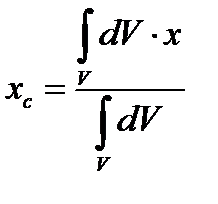 ;
; 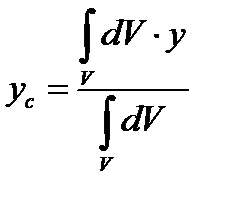 ;
; 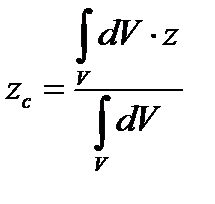 ;
;
де, 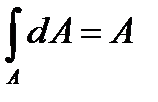 - повна площа фігури.
- повна площа фігури.
5. Для визначення центра тяжіння плоского тіла складної форми, тіло ділять на елементарні площі. Маса однорідного тіла пропорційна його елементарній площі.
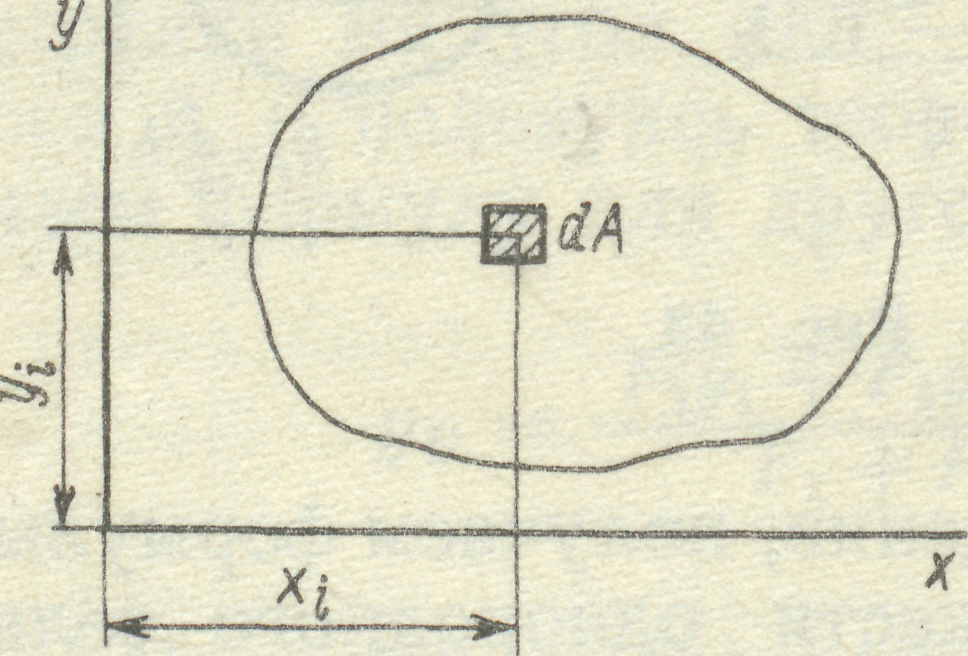 Добуток елементарної площі фігури на відстань від її центра ваги до будь-якої вісі називається статичним моментом ваги (рис.15).
Добуток елементарної площі фігури на відстань від її центра ваги до будь-якої вісі називається статичним моментом ваги (рис.15).
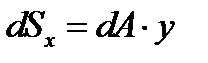 ;
;
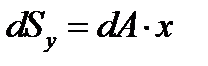 .
.
Сума статичних моментів всіх частин фігури називається статичним моментом площі фігури відносно даної вісі.
Рис. 15 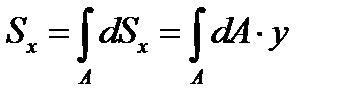 ;
;
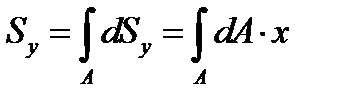 .
.
Статичний момент площі визначається одиницями довжини в третьому ступені ( 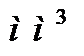 ,
, 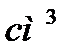 ,
, 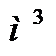 ).
).
Якщо початок координат розмістити в центрі тяжіння площини, то статичні мо-менти відносно осей 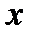 та
та 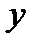 , які проходять через центр тяжіння, будуть дорівнювати нулю. Відповідно статичний момент плоскої фігури відносно будь-якої центральної вісі дорівнює нулю.
, які проходять через центр тяжіння, будуть дорівнювати нулю. Відповідно статичний момент плоскої фігури відносно будь-якої центральної вісі дорівнює нулю.
6.Полярним моментом інерції перерізу називається взята по всьому перерізу сума добутків або інтеграл елементарних площ на квадрати їх відстаней від деякої точки О до перерізу (рис. 16а).
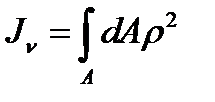 .
.
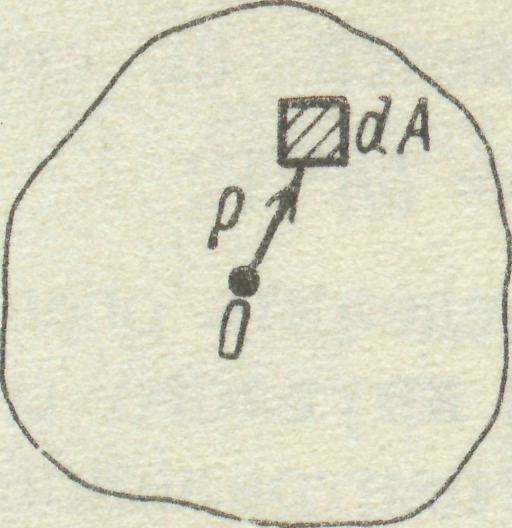
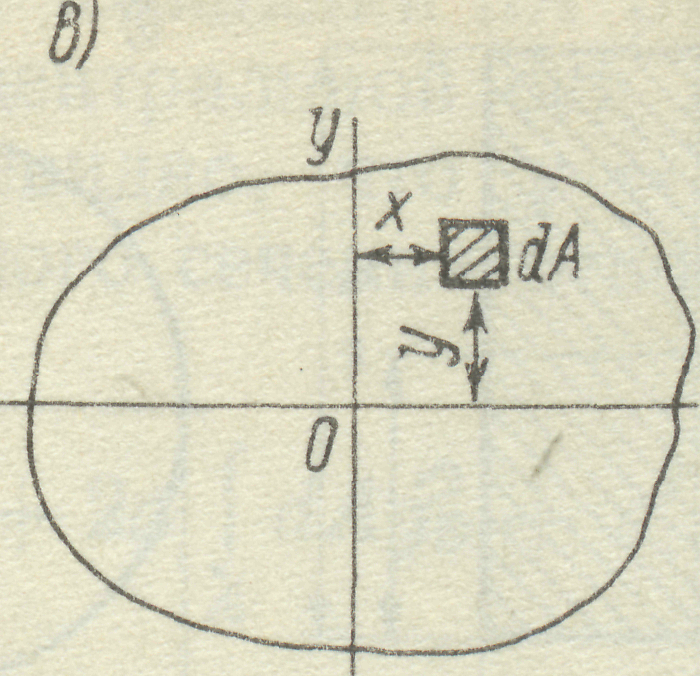
а б
Рис. 16
Осьовим моментом інерції перерізу називається взята по всьому перерізу сума добутків або інтеграл елементарних площ на квадрати їх відстаней до деякої вісі, яка лежить в площині перерізу, який розглядається (рис. 16б).
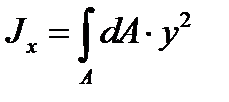 ;
;
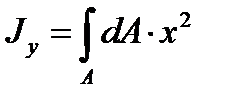 .
.
Значення осьового моменту служить характеристикою здатності балки опиратись згину.
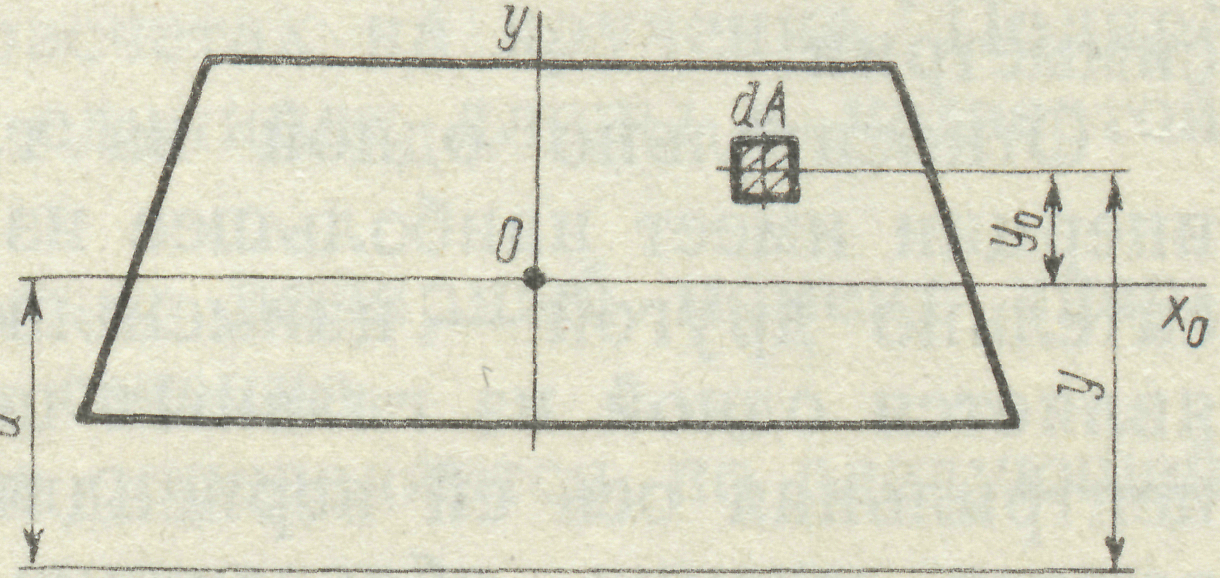 7. Для обчислення осьових моментів інерції складних перерізів користуються тео-ремою про моменти інерції відносно паралельних осей. Момент інерції перерізу відносно вісі, яка не проходить через його центр ваги, дорівнює сумі моментів інерції перерізу відносно його централь-ної вісі, яка паралельна даній вісі, та добутку площі перерізу на квадрат відстані між осями (рис. 17).
7. Для обчислення осьових моментів інерції складних перерізів користуються тео-ремою про моменти інерції відносно паралельних осей. Момент інерції перерізу відносно вісі, яка не проходить через його центр ваги, дорівнює сумі моментів інерції перерізу відносно його централь-ної вісі, яка паралельна даній вісі, та добутку площі перерізу на квадрат відстані між осями (рис. 17).
Рис. 17 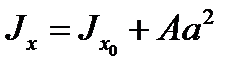 .
.
Дата добавления: 2015-04-03; просмотров: 2982;
