Про співвідношення маси і енергії

На початку Фейнманівської лекції зі спеціальної теорії відносності, наведеній у томі 2, декларується, що „Ейнштейн виправив помилку Ньютона в тому, що маса вважалася сталою. І що тепер ми знаємо, що це не так, що маса тіла зростає із збільшенням швидкості”. Невдало вжита фраза виявилась живучою настільки, що спростування її відбувається до наших днів. Так в статті Л.Б.Окуня „понятие массы. (Масса, энергия, относительность)”, яка вийшла в журналі „Успехи физических наук” у 1989 році, автор доводить читачам, що правильними твердженнями слід вважати такі. Маса тіла 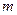не змінюється при його русі, а величина добутку маси на квадрат швидкості світла у вакуумі рівна енергії, зосередженій в тілі, що покоїться, тобто 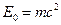. При цьому вживання крім терміна маса ще і терміна маса спокою є зайвим. Замість „маса спокою” слід говорити про масу тіла 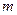, яка для звичайних тіл і в теорії відносності, і в Ньютонівській механіці одна й та ж сама. В обох теоріях маса 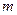не залежить від системи відліку, а помилкове тлумачення, що нібито маса залежить від швидкості руху тіла, виникло внаслідок незаконного перенесення Ньютонівського співвідношення між імпульсом і швидкістю 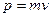в область швидкостей, близьких до швидкості світла, в якій це співвідношення несправедливе.

Яким повинен бути вираз для імпульсу в релятивістській області це питання вирішувалося вимогою задовольнити умову збереження імпульсу, тобто щоб закон збереження імпульсу був інваріантним по відношенню до перетворень Лоренца. Виявилось, що імпульс, який задовольняє цим вимогам, має вигляд

.

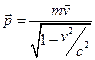Ясно, що інваріантним до перетворень Лоренца тепер став і другий закон Ньютона (або просто рівняння Ньютона)

.

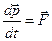Підкреслимо, що у виразі для імпульсу маса 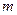та ж сама, що фігурує і в другому законі Ньютона, який раніше застосовувався для нерелятивістської області.

Якщо тепер спробувати отримати вираз для кінетичної енергії окремої частинки, вважаючи як завжди, що приріст її обумовлений елементарною роботою результуючої всіх сил, що діють на частинку, то одержимо

.

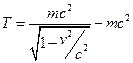Але є підстави приписати вільній частинці крім кінетичної енергії так звану енергію спокою 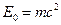. Таким чином, повна енергія вільної частинки визначається виразом

.

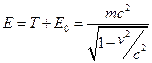Тією підставою для врахування 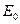у виразі є вимога виконання закону збереження енергії у всіх інерціальних системах відліку. При розгляді системи частинок, які співударяються, виявилось, що зберігається саме сума (за кількістю частинок) виразів, що мають вигляд 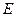. Як і в Ньютонівській механіці, енергія, так само як і імпульс, адитивні величини: повні енергія і імпульс вільних частинок рівні відповідно

, .

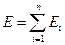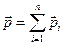Якщо із рівнянь і виключити швидкість 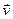, отримаємо вирази для повної енергії і імпульсу, які є основними співвідношеннями теорії відносності для частинки, що вільно рухається (і системи частинок)

,

.

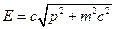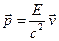Слід ще раз підкреслити, що маса 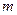і швидкість 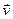для частинки або системи це ті ж самі величини, з якими ми маємо справу в Ньютонівській механіці. І в теорії відносності маса ізольованої системи зберігається, не змінюється з часом. Правда, при цьому в число тіл, що складають систему, треба включити не тільки речовину (атоми), а й випромінювання (фотони). Але властивості адитивності маса вже не має: маса цілого не дорівнює сумі мас складових цього цілого.

Найважливішою відмінністю теорії відносності від нерелятивістської механіки є те, що енергія масивного тіла не обертається в нуль, навіть за умови, що воно знаходиться в стані спокою, тобто, коли , .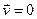

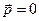Тут терміном „масивне тіло” позначена частинка, що має масу, на відміну від фотона, у якого маса рівна нулю. Як видно з формули , енергія спокою тіла, яку позначаємо 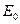, пропорційна його масі

.

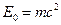Саме твердження про те, що в нерухомій матерії зосереджений колосальний (завдяки квадрату швидкості світла 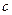) запас енергії, зроблене Ейнштейном у 1905 році являється головним практичним висновком теорії відносності. Співвідношення є обгрунтуванням всієї ядерної енергетики, в тому числі військової ядерної техніки, і що можливо мало кому відомо, навіть звичайної енергетики.

В ядерних і хімічних реакціях енергія спокою відповідно до закону збереження енергії повинна переходити у кінетичну енергію продуктів реакції , якщо сумарна маса частинок, що вступають в реакцію, більша за сумарну масу продуктів реакції. Частина маси, що втрачається (дефект маси), перетворюється в енергію за формулою 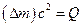. Наведемо декілька прикладів.

1. При анігіляції електрона і позитрона з народженням двох фотонів вся енергія спокою електрона і позитрона переходить в кінетичну енергію фотонів

.

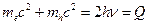Тут 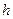– стала планка, 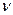– частота світла.

2. При зіштовхуванні з ядром урану повільного нейтрона ядро розщеплюється на два осколки, наприклад, за схемою

.

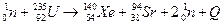При цьому вилітають 2 нейтрони, здатних розщепити інші ядра урану, і виділяється енергія .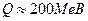

Враховуючи маси всіх частинок одержимо, що відносне зменшення маси продуктів цієї реакції становить

.

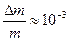3. В реакції спалювання метану на газовій плитці 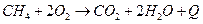виділяється енергія 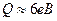. Легко знайти, що в цьому випадку 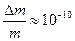. В хімічних реакціях величина 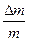на 7-8 порядків менша, ніж в ядерних, але суть механізму виділення енергії та ж сама: енергія спокою переходить у кінетичну енергію.