Затухаючі коливання
Затухаючі коливання описуються рівнянням (дивись )
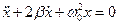 .
.
Розв’язок шукаємо у вигляді 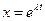 . Підставляючи похідні
. Підставляючи похідні 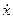 і
і 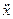 в отримаємо характеристичне рівняння
в отримаємо характеристичне рівняння
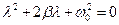 ,
,
коренями якого є
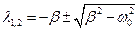 .
.
Якщо затухання не дуже велике (коли 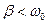 ), то вираз під радикалом буде від’ємним. Позначимо його
), то вираз під радикалом буде від’ємним. Позначимо його 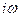 , де
, де 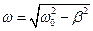 .
.
Тоді згідно загальний розв’язок рівняння матиме вигляд
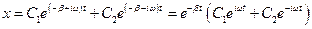 .
.
Вираз в дужках аналогічний виразу , тому його можна представити у вигляді . Тоді маємо розв’язок рівняння затухаючих коливань
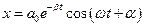 .
.
Тут 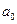 і
і 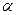 – довільні сталі.
– довільні сталі.
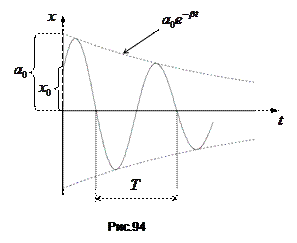 На рис.94 приведений графік функції . Рух, заданий , можна розглядати як гармонічне коливання з частотою
На рис.94 приведений графік функції . Рух, заданий , можна розглядати як гармонічне коливання з частотою 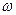
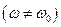 і амплітудою
і амплітудою 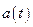 , яка змінюється з часом по закону
, яка змінюється з часом по закону 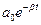 . Верхня пунктирна крива на рис.94 є графіком функції
. Верхня пунктирна крива на рис.94 є графіком функції 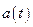 , де
, де 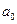 – амплітуда в початковий момент часу. Початкове зміщення
– амплітуда в початковий момент часу. Початкове зміщення 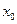 залежить крім
залежить крім 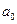 ще і від початкової фази
ще і від початкової фази 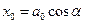 . Швидкість затухання коливань характеризується величиною
. Швидкість затухання коливань характеризується величиною 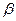 , яка називається коефіцієнтом затухання. Знайдемо час
, яка називається коефіцієнтом затухання. Знайдемо час 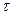 , за який амплітуда зменшиться в
, за який амплітуда зменшиться в 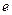 разів.
разів. 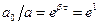 , звідси
, звідси 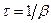 .
.
За формулою запишемо вираз для періоду затухаючих коливань
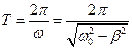 .
.
При малих опорах середовища 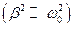 період
період 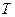 майже стала величина
майже стала величина 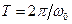 , а із збільшенням коефіцієнта затухання період коливань збільшується.
, а із збільшенням коефіцієнта затухання період коливань збільшується.
Введемо логарифмічний декремент затухання 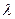 як логарифм відношення амплітуд, які відрізняються одна від одної через період
як логарифм відношення амплітуд, які відрізняються одна від одної через період
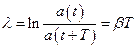 .
.
Саме логарифмічний декремент 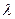 використовується для характеристики коливної системи. За допомогою зменшення амплітуди можна записати так
використовується для характеристики коливної системи. За допомогою зменшення амплітуди можна записати так
 .
.
За час 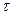 , коли амплітуда зменшиться в
, коли амплітуда зменшиться в 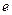 разів, нехай відбулося
разів, нехай відбулося  коливань
коливань 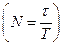 . Тоді на підставі умови
. Тоді на підставі умови
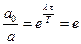
одержуємо
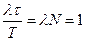 .
.
Таким чином, логарифмічний декремент затухання 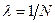 дорівнює величині, оберненій кількості коливань, які відбулися до зменшення амплітуди в
дорівнює величині, оберненій кількості коливань, які відбулися до зменшення амплітуди в 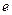 разів.
разів.
Для характеристики коливної системи часто використовується також величина 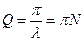 , яка називається добротністю коливної системи.
, яка називається добротністю коливної системи.
Із формули випливає, що із зростанням коефіцієнта затухання 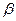 період коливань
період коливань 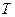 збільшується і при
збільшується і при 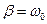 , період коливань обертається в нескінченність, тобто рух стає неперіодичним.
, період коливань обертається в нескінченність, тобто рух стає неперіодичним.
При 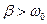 корні характеристичного рівняння стають дійсними, а тому розв’язок диференціального рівняння буде мати вигляд
корні характеристичного рівняння стають дійсними, а тому розв’язок диференціального рівняння буде мати вигляд
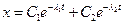 ,
,
 де
де 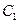 і
і  – дійсні сталі, величини яких залежать від початкових умов (значень
– дійсні сталі, величини яких залежать від початкових умов (значень 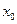 і
і 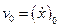 ).
).
З останнього рівняння випливає, що рух є аперіодичним, – система повертається в стан рівноваги без коливань. На рис.95 показані два можливих способи повернення системи в положення рівноваги. Який саме рух реалізується залежить від початкових умов. Рух, показаний кривою 2 наприклад, можливий при наявності сильного поштовху кульки в напрямку положення рівноваги.
Дата добавления: 2015-06-17; просмотров: 1338;
