Складання взаємно-перпендикулярних коливань

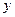Припустимо, частинка може коливатися вздовж осі і вздовж перпендикулярної до неї осі . Тоді в загальному випадку частинка буде рухатися в площині по криволінійній траєкторії, форма якої залежатиме від різниці фаз обох коливань.

Виберемо початок відліку часу так, щоб початкова фаза першого коливання (вздовж осі ) була рівна нулю. Тоді рівняння коливань запишуться так

де 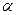– різниця фаз обох коливань. Щоб знайти рівняння траєкторії, виключимо 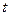в рівняннях

, .

Розкриваємо косинус в другому рівнянні

.

Після підстановки виразів отримаємо

.

Останнє рівняння після нескладних перетворень приводить, взагалі кажучи, до рівняння еліпса, вісі якого повернуті відносно координатних осей і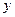

.

Визначимо траєкторію руху в окремих випадках.

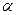1. Різниця фаз дорівнює нулю. Тоді рівнянням траєкторії є рівняння прямої (рис.92)

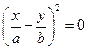або .

Результуючий рух є гармонічним коливанням вздовж цієї прямої з частотою 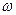і амплітудою .

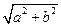2. Різниця фаз 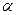дорівнює 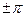. З отримаємо рівняння прямої 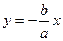. Результуючим рухом буде гармонічне коливання вздовж цієї прямої.

3. При 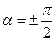рівняння набуває вигляду

.

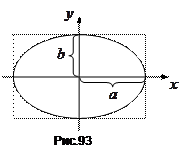
Це є рівняння еліпса, приведене до координатних осей (рис.93). Напрям руху частинки по еліпсу легко визначити з рівнянь . При рух відбуватиметься по годинниковій стрілці, а при – проти годинникової стрілки.

Якщо частоти взаємно-перпендикулярних коливань неоднакові, то в загальному випадку, траєкторіями будуть складні криві, які називаються фігурами Ліссажу.