Додавання взаємно перпендикулярних гармонічних коливань.

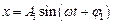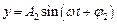Спочатку розглянемо додавання взаємно перпендикулярних гармонічних коливань однакової частоти. Нехай точка М одночасно здійснює коливання вздовж осей координат ОХ і ОY за законами: і , де x і y – декартові координати точки М. Рівняння траєкторії результуючого руху точки М у площині ХОY можна знайти, якщо виключити з виразів і 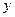параметр ,

.

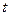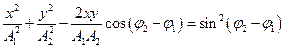Траєкторія має форму еліпса (рис.9.11), причому точка М описує даний еліпс за час, який дорівнює періоду доданих коливань 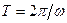. Тому результуючий рух точки М називають еліптично поляризованими коливаннями.

Орієнтація в площині ХОY осей еліпса, а також його розміри залежать від амплітуд А₁ і А₂ доданих коливань і різниці їх початкових фаз 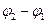. Якщо 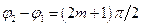, де 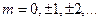, то осі еліпса збігаються з осями координат ОХ і ОY, а розміри його напівосей дорівнюють амплітудам 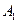і :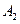

.

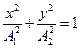Якщо, крім того, 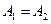, то траєкторія точки М являє собою коло. Такий результуючий рух точки М називають циркулярно поляризованими коливаннями, або коливаннями поляризованими по колу.

У тих випадках, коли 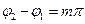, де 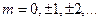, еліпс вироджений у відрізок прямої:

.

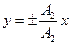Знак плюс відповідає парним значенням m, тобто додаванню синфазних коливань (рис.9.12,а), а знак мінус – непарним значенням m, тобто додаванню коливань, що здійснюються в протифазі (рис.9.12,б). В таких випадках точка М здійснює лінійно поляризовані коливання. Вона гармонічно коливається з частотою 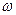і амплітудою 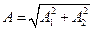вздовж прямої лінії, яка складає з віссю ОХ кут .

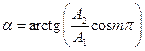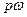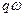Розглянемо додавання взаємно перпендикулярних коливань з циклічними частотами і , де 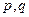– цілі числа:

, .

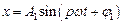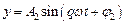Значення координат х і y точки М, яка здійснює коливання, одночасно повторюються через однакові проміжки часу Т₀, які дорівнюють загальному найменшому кратному 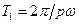і 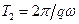– періодів коливань вздовж осей ОХ і ОY. Тому траєкторія точки М – замкнена крива, форма якої залежить від співвідношення амплітуд, частот і початкових фаз коливань, що додаються. Такі замкнені траєкторії точки М, яка здійснює гармонічні коливання одночасно в двох взаємно перпендикулярних напрямках, називаються фігурами Лісажу. Фігури Лісажу вписані в прямокутник, центр якого збігається з початком координат, а сторони паралельні осям координат осей ОХ і ОY і розташовані по обидва боки від них на відстанях, відповідно рівних А₂ і А₁. Відношення частот pw і qw коливань, що додаються, дорівнює відношенню кількості дотиків відповідної фігури Лісажу зі стороною прямокутника, яка паралельна осі ОY, і зі стороною, яка паралельна осі ОХ. На рис.9.13 наведено вигляд фігур Лісажу при трьох різних відношеннях 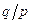(2:1, 3:2 і 4:3).

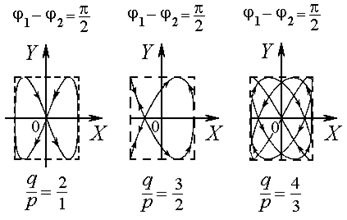
Рис. 9.13.