Загасальні коливання

Загасанням коливань називається поступове ослаблення коливань з часом, яке зумовлено втратою енергії коливальною системою. Вільні коливання реальних систем завжди затухають. Затухання вільних механічних коливань викликано головним чином тертям і збудженням в навколишньому середовищі пружних хвиль.

Закон загасання коливань залежить від властивостей коливальної системи. Система називається лінійною, якщо параметри, що характеризують в певному процесі існуючі фізичні властивості системи, не змінюються. Лінійні системи описуються лінійними диференційними рівняннями. Наприклад, пружинний маятник, що рухається у в’язкому середовищі, являє собою лінійну систему, якщо коефіцієнт опору середовища і пружність пружини не залежать від швидкості і зміщення маятника.

Отримаємо диференційне рівняння, яке описує загасальні коливання. З цією метою запишемо рівняння руху матеріальної точки (другий закон Ньютона) з врахуванням сил опору. Розглянемо типовий випадок, коли сила опору 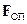залежить від швидкості руху точки і при малих швидкостях її можна вважати пропорційною швидкості v: , де r – коефіцієнт пропорційності. Знак мінус означає, що сила опору спрямована в бік, протилежний до напрямку руху точки. Якщо рух здійснюється вздовж напрямку , то . Ця сила додається до пружної сили 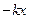, отже другий закон Ньютона набуде вигляду:

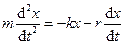
або

,

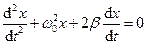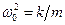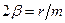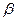де і , – коефіцієнт затухання, 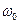– циклічна частота вільних незагасальних коливань тієї ж системи за відсутності втрат енергії ( ).

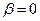У випадку не дуже сильного загасання ( 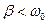) розв’язком даного рівняння є:

,

де 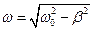, 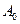і 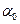– константи, які визначаються з початкових умов, тобто значень і 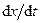в момент часу 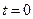. Графік залежності від часу наведено на рис.9.14. Як видно, коливання загасають з часом.

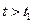Загасальні коливання не є строго періодичними. Наприклад, максимальне значення величини , яке досягається в певний момент часу (див. рис.9.14) надалі ( ) ніколи не повториться. Проте, при загасальних коливаннях величина стає рівною нулеві, а також набуває максимальних і мінімальних значень через рівні проміжки часу:

.

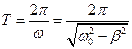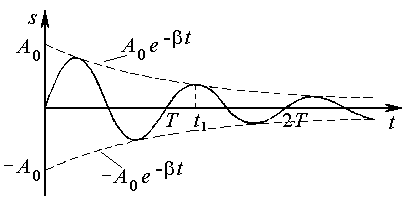Рис. 9.14.

Тому величини 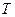і 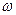умовно називають періодом (умовним періодом) і циклічною частотою (умовною циклічною частотою) загасальних коливань.

Величина 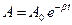називається амплітудою загасальних коливань, а 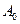– початковою амплітудою. Амплітуда загасальних коливань зменшується з часом тим сильніше, чим більший коефіцієнт затухання 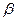(втрати енергії системою). Проміжок часу 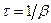, за який амплітуда загасальних коливань зменшується в е разів, називається часом релаксації.

Загасальні коливання характеризують логарифмічним декрементом загасання та добротністю коливальної системи. Логарифм відношення двох послідовних значень амплітуд, які віддалені одне від одного на час, рівний періоду 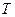, називається логарифмічним декрементом загасання:

.

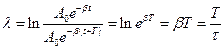Добротністю коливальної системи називається безрозмірна фізична величина 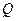, що дорівнює добутку на відношення енергії коливальної системи у довільний момент часу 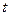до зменшення цієї величини за проміжок часу від 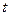до 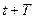, тобто за один умовний період загасальних коливань:

.

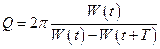Оскільки енергія пропорційна квадрату амплітуди коливань 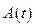, вираз для добротності системи можна представити у вигляді

.

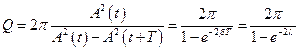· При малих 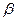добротність коливальної системи . При цьому умовний період 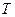загасальних коливань практично дорівнює періоду 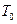власних незагасальних коливань, і добротність дорівнює

.

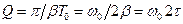· При збільшенні 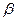умовний період загасальних коливань збільшується і обертається у нескінченність при .

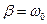· При 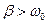загальний розв’язок диференційного рівняння коливальної системи набуває такого вигляду:

,

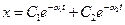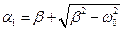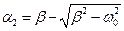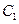де , , а і 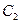– сталі коефіцієнти, які визначаються з початкових умов. Якщо початкові значення (в момент часу 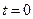) 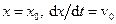, то

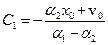і .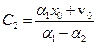

Такий рух системи не є коливальним і називається аперіодичним. Система повертається в рівноважний стан ( 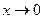) без здійснення коливань. При цьому характер руху залежить від початкових умов. Так, можливі два типи аперіодичного руху системи (рис.9.15). Рух типу а відбувається у тих випадках, коли 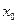і 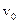протилежні за знаком і .

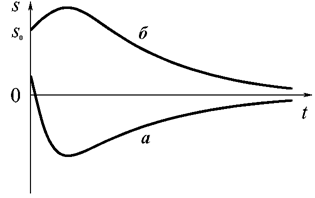
Рис. 9.15.