Рівняння хвилі

Поняття хвилі (чи хвильового процесу) є одним з фундаментальних понять фізики. Хвильові процеси широко зустрічаються у природі. Деякі з них добре відомі нам з повсякденного життя. Незважаючи на це, сприйняття цього фізичного поняття викликає певні труднощі, головним чином пов’язані із застосуванням математичного апарату. Щоб полегшити сприйняття хвиль як концепційного фізичного поняття, розглянемо декілька прикладів.

Під хвильовим процесом надалі будемо розуміти процес розповсюдження збурень у просторі з певною скінченною швидкістю. Фізичні процеси, які зумовлюють розповсюдження збурення від точки до точки, бувають різні. Наприклад, це можуть бути процеси взаємного перетворення електричного і магнітного полів. Такі хвилі ми звикли називати електромагнітними. При цьому під збуренням, яке розповсюджується, зазвичай розуміють фізичну величину напруженості електричного чи магнітного поля. Ще один приклад. У багатьох середовищах при зміщенні частинок речовини у просторі виникають сили, що діють на сусідні частинки і вимушують їх змінювати свої положення. Завдяки цьому у середовищі відбувається хвильовий процес, який ми називаємо механічні хвилі. Відомий приклад механічних хвиль – звукові хвилі, які виникають у пружних середовищах.

Хвильові процеси можна описати аналітично, якщо знати величину збурення в кожний момент часу для кожної точки простору. Такий опис здійснюється за допомогою так званого рівняння хвилі.

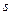Спочатку розглянемо спрощену одновимірну задачу – розповсюдження хвиль уздовж виділеного напрямку, наприклад, уздовж осі . Припустимо, деяка фізична величина визначена на вісі . Згідно із загальним означенням, будь-яка одновимірна біжуча хвиля, що розповсюджується у напрямку , математично може бути представлена функцією

,

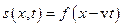де 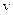- швидкість її розповсюдження. Відповідно, хвиля, що розповсюджується у протилежному напрямку, записується як 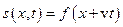. Наведені вирази називаються рівняннями хвилі. Слід підкреслити, що функція 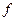може бути довільною. Незважаючи на простоту формулювання, наведене означення не просте для розуміння. Розглянемо декілька прикладів біжучих хвиль.

Приклад 1. Рівняння хвилі описує одновимірну біжучу хвилю. Цю хвилю можна наочно представити графічно. Уявіть собі графік функції 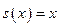- він представляє собою пряму лінію. Графік функції 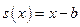, очевидно, представляє собою графік функції 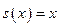, зміщений по осі на величину 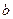. Тоді стає зрозумілим, що функція представляє собою функцію 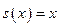, яка рухається у напрямку з швидкістю 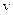. Очевидно, вираз 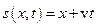описує аналогічну хвилю, що рухається у протилежному напрямку (у напрямку ).

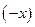Приклад 2. Розглянемо відому функцію Гауса 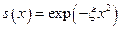. Її графік представляє собою симетричну плавну криву з максимумом (колоколоподібний імпульс). Якщо у функції Гауса в якості аргументу взяти комбінацію 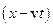, то утворений вираз 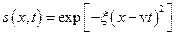згідно з означенням буде біжучою хвилею. Ця хвиля представляє собою поодинокий імпульс, який рухається у напрямку з швидкістю 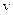. (Примітка. Тут 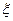- стала величина, яка введена у формулу Гауса з міркувань розмірностей, тобто для того, щоб під експонентою був безрозмірний вираз.)

Приклад 3. Хвиля 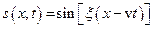представляє собою біжучу нескінченну синусоїду. Очевидно, ця хвиля є математичною абстракцією, оскільки реально нескінченних синусоїд не існує. Слід зазначити також, що, на відміну від двох попередніх прикладів, ця хвиля – не поодинока, а періодична. Періодичні хвилі часто зустрічаються у природі.

У щойно розглянутому прикладі, аргумент функції синуса часто записують наступним чином. Вводять так зване хвильове число, 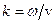, де 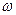- кругова частота, 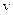- швидкість розповсюдження хвилі. Тоді синусоїдальну (або косинусоїдальну) біжучу хвилю можна представити, наприклад, як

,

де 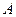- амплітуда.

Крім поодиноких хвиль (імпульсів) та нескінченних періодичних хвиль часто використовується поняття цуг хвиль. Під цугом хвиль звичайно розуміють обмежену послідовність повторювальних збурень, наприклад, послідовність із скінченної кількості імпульсів або обмежений фрагмент синусоїди з обмеженою кількістю періодів.

Розглянуті приклади являють собою так звані одновимірні хвилі. Якщо ж розглядувана фізична величина 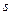визначена не тільки на вісі , а в усьому просторі, то наведені приклади рівнянь хвиль набувають ширшого змісту – це так звані плоскі хвилі, які розповсюджуються уздовж осі . Для таких плоских хвиль характерно, що 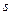не залежить від координат , а залежить лише від координати .

Хвиля називається монохроматичною (або гармонічною), якщо величина збурення, 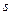, в кожній точці простору здійснює гармонічні коливання. Особливий інтерес становить плоска гармонічна (або монохроматична) хвиля. Рівняння плоскої монохроматичної хвилі, що розповсюджується уздовж вісі , має вигляд, наприклад,

.

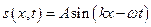Якщо виникає потреба записати рівняння монохроматичної плоскої хвилі, яка розповсюджується не вздовж вісі , а у довільному заданому напрямку, тоді замість хвильового числа 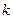застосовують так званий хвильовий вектор . Модуль хвильового вектора дорівнює хвильовому числу, 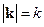, а напрямок хвильового вектора вказує напрямок розповсюдження хвилі. Тоді рівняння плоскої монохроматичної хвилі, яка розповсюджується уздовж вектора , можна записати, наприклад, як

.

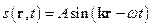Отримане рівняння плоскої монохроматичної хвилі можна записати в експоненційній формі, якщо використати формулу Ейлера:

.

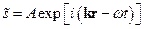Експоненційна форма зручніша для математичної обробки. Фізичний зміст має лише дійсна частина комплексної величини 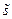, тобто величина . Тому, після використання величини 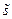для знаходження певного параметра хвилі слід відкинути уявну частину отриманого комплексного виразу, яка позбавлена фізичного змісту.

Величина 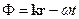, яка є аргументом функції синуса або косинуса у рівнянні плоскої монохроматичної хвилі, називається фазою плоскої хвилі. Хвильовою поверхнею, або фронтом хвилі, називається геометричне місце точок, в яких фаза хвилі має однакове значення. Множині різних величин фази відповідає сімейство хвильових поверхонь. Хвильові поверхні плоских хвиль являють собою сукупність паралельних площин, перпендикулярних до напрямку розповсюдження хвилі.

Крім згаданих плоских хвиль існують ще й інші типи хвиль. Важливим типом хвиль є так звані сферичні хвилі, для яких поверхня рівної фази є сферою, а хвильові поверхні мають вигляд концентричних сфер. Центри цих сфер називаються центром хвилі. Сферичні хвилі збуджуються в однорідному ізотропному середовищі точковим джерелом. Рівняння сферичної хвилі має такий вигляд:

,

де 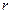– відстань від центру хвилі до розглядуваної точки середовища, 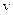– швидкість розповсюдження хвилі. Характерна особливість рівняння сферичної хвилі – наявність множника .

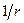Для сферичної монохроматичної хвилі можна записати

,

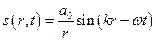де 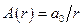– амплітуда хвилі, 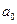– фізична величина, яка чисельно дорівнює амплітуді хвилі на одиничній відстані від її центра. З наведеного виразу видно, що амплітуда 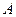гармонічних коливань величини 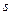зменшується з віддаленням від джерела хвиль за законом .

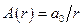Рівняння сферичної монохроматичної хвилі можна записати в експоненційній формі:

.

Слід відзначити, що реальні джерела хвиль завжди мають певні розміри. Їх можна вважати точковими, а збуджені ними хвилі сферичними лише за умови, якщо відстань 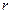від джерела хвиль значно більша за розміри джерела. При дуже великих 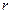будь-які невеликі ділянки сферичної хвильової поверхні можна вважати плоскими.