Хвильове рівняння
При розгляді багатьох фізичних задач, виходячи з фундаментальних фізичних законів шляхом математичних перетворень, отримують диференціальні рівняння, які описують розглядувані фізичні процеси. Наприклад, якщо застосувати фундаментальний фізичний закон – другий закон Ньютона – до задачі про рух маятника в однорідному полі тяжіння, можна отримати наступне диференціальне рівняння
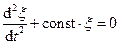 .
.
Як було показано у попередньому розділі, рівняння такого вигляду зустрічаються у багатьох фізичних задачах і описують гармонічні коливання величини, яка у рівнянні позначена 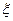 . При цьому в різних задачах в якості
. При цьому в різних задачах в якості 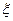 виступають різні фізичні величини (координата важеля, кут повороту, електричний заряд, напруженість поля, та ін.), а константа у рівнянні, хоча і набуває різних значеннь в різних задачах, але завжди має той же самий фізичний зміст – це квадрат кругової частоти власних коливань. Отже, вищенаведене рівняння є начебто візитною карткою різноманітних процесів, які ми називаємо спільною назвою “гармонічні коливання”. Розв’язками цього рівняння є такі відомі вирази, як, наприклад,
виступають різні фізичні величини (координата важеля, кут повороту, електричний заряд, напруженість поля, та ін.), а константа у рівнянні, хоча і набуває різних значеннь в різних задачах, але завжди має той же самий фізичний зміст – це квадрат кругової частоти власних коливань. Отже, вищенаведене рівняння є начебто візитною карткою різноманітних процесів, які ми називаємо спільною назвою “гармонічні коливання”. Розв’язками цього рівняння є такі відомі вирази, як, наприклад, 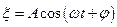 та
та 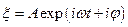 .
.
З рівняннями, які описують хвильові процеси, складається ситуація, аналогічна коливальним процесам. У різноманітних фізичних задачах, які розглядають різні хвильові процеси, з фізичних законів випливає одне й те саме диференціальне рівняння, яке в подальшому ми будемо називати хвильовим рівнянням. В одновимірному випадку це рівняння має вигляд
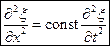 .
.
На відміну від гармонічних коливань, хвильове рівняння – це рівняння у частинних похідних. Розв’язками цього хвильового рівняння є вищерозглянуті рівняння хвилі 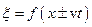 , у тому числі рівняння гармонічних хвиль. У цьому можна впевнитись шляхом підстановки функції
, у тому числі рівняння гармонічних хвиль. У цьому можна впевнитись шляхом підстановки функції 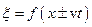 у хвильове рівняння. Для скорочення запису тимчасово позначимо
у хвильове рівняння. Для скорочення запису тимчасово позначимо 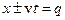 . Приймемо до уваги, що
. Приймемо до уваги, що 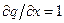 ,
, 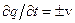 , і перетворимо похідні:
, і перетворимо похідні:
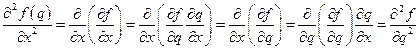 ,
,
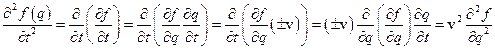 .
.
Підставимо отримані вирази для похідних у хвильове рівняння і отримаємо:
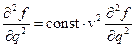 .
.
Таким чином, стає зрозумілим фізичний зміст константи у хвильовому рівнянні - рівняння перетворюється на тотожність за умови 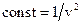 , де
, де 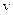 - швидкість розповсюдження хвилі.
- швидкість розповсюдження хвилі.
У тривимірному випадку хвильове рівняння записують у вигляді
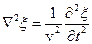 ,
,
де оператор Лапласа 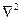 у декартових координатах має вигляд
у декартових координатах має вигляд
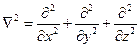 .
.
Для сферичних хвиль рівняння хвилі виглядає аналогічно, тільки оператор Лапласа повинен бути перетворений за правилами переходу до сферичної системи координат. Наприклад, хвильове рівняння для сферичних хвиль можна подати у вигляді
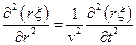 .
.
Дата добавления: 2015-04-07; просмотров: 2529;
