Інтерференція хвиль. Стоячі хвилі

Спостереження над хвилями, які поширюються від двох джерел і накладаються одна на одну, показали, що кожна з хвиль не впливає на поширення іншої. В цьому полягає принцип суперпозиції, або принцип накладання хвиль. Зміщення кожної точки середовища в будь-який момент часу при накладанні однієї хвилі на іншу можна отримати шляхом геометричного додавання зміщень, викликаних кожною з хвиль окремо.

Якщо ці зміщення паралельні і хвилі мають однакову довжину, тобто коливання частинок середовища мають однакові частоти, то результуюче коливання частинки буде відбуватись з тією ж частотою. Проте, амплітуди і фази коливань у різних частинок будуть різними, оскільки вони залежать не тільки від амплітуд коливань в певній точці, але і від різниці фаз коливань, які накладаються. Нехай початкові фази джерел коливань однакові. В такому випадку різниця фаз коливань певної частинки середовища, яка спостерігається при накладанні хвиль, залежить від різниці відстаней джерел хвиль до неї, тобто від різниці ходу хвиль від джерел до точки, в якій визначається результат накладання хвиль. Якщо різниця ходу дорівнює парній кількості половин довжини хвилі (напівхвиль), то фази коливань будуть однакові і результуюча амплітуда буде дорівнювати сумі амплітуд коливань, які накладаються.

У випадку, коли різниця фаз дорівнює непарній кількості напівхвиль, то різниця фаз коливань буде дорівнювати 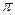і при накладанні хвиль їх амплітуди будуть відніматись. За умови рівності амплітуд в такій точці середовища коливань не буде – коливання, зумовлені однією хвилею, будуть знищені (компенсовані) коливаннями іншої.

Дві хвилі є когерентними, якщо різниця їх фаз не залежить від часу. Когерентним хвилям відповідають когерентні коливання, а їх джерела, відповідно, називають когерентними джерелами. Монохроматичні хвилі з однаковими частотами завжди когерентні. Монохроматичні хвилі з різними частотами некогерентні.

При накладанні некогерентних монохроматичних хвиль, які збуджуються джерелами S₁ і S₂ (рис.10.2), квадрат амплітуди А результуючих негармонічних коливань в довільній точці М періодично змінюється з часом t за законом:

,

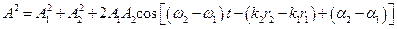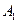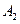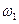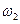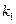тут і , і 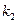, 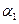і , і 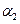– амплітуди в точці М, циклічні частоти, хвильові числа і початкові фази обох сферичних хвиль, що накладаються. Період зміни 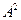дорівнює 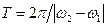. Середня за період величина квадрата амплітуди:

.

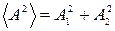Отже при накладанні некогерентних хвиль відбувається додавання квадратів їх амплітуд (інтенсивностей).

Інтерференцією хвиль називають явище накладання хвиль, при якому відбувається незмінне в часі їхнє взаємне посилення в одних точках простору та послаблення в інших в залежності від співвідношення між фазами цих хвиль. Інтерференція спостерігається лише для когерентних хвиль, яким відповідають коливання, що здійснюються вздовж одного і того самого або близьких напрямків.

При накладанні когерентних сферичних хвиль, які збуджуються джерелами S₁ і S₂ (рис.10.2),

,

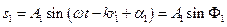
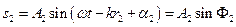амплітуда 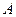і фаза 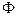результуючих гармонічних коливань в точці М визначаються співвідношеннями:

,

.

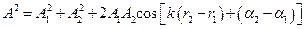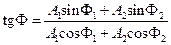Оскільки для коливань когерентних джерел різниця початкових фаз 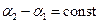, то результат інтерференції двох хвиль в різних точках М залежить від величини 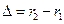, яка називається різницею ходу хвиль. В інтерференційних максимумах амплітуда результуючих коливань 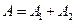, а в мінімумах 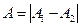. Максимуми будуть спостерігатись в точках М середовища, для яких виконується умова:

,

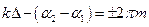де 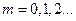– порядок інтерференційного максимуму.

Умова спостереження мінімуму є наступною:

,

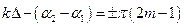де 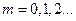– порядок інтерференційного мінімуму.

Оскільки хвильове число 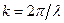, де 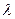– довжина хвилі в даному середовищі, то умови інтерференційних максимумів і мінімумів можна подати в іншому вигляді:

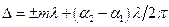– максимуми,

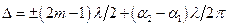– мінімуми,

Якщо ж 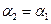, наведені умови мають такий вигляд:

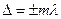- максимуми,

тобто максимум амплітуди виникає в точках середовища, для яких різниця ходу хвиль дорівнює нулеві або цілому числу довжин хвиль (або, що те саме, парній кількості напівхвиль), і

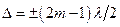- мінімуми,

тобто мінімум амплітуди виникає в точках середовища, для яких різниця ходу хвиль дорівнює непарній кількості напівхвиль.

Відзначимо, що при інтерференції не відбувається простого додавання енергій хвиль. В інтерференційних максимумах інтенсивність результуючої хвилі більша суми інтенсивностей хвиль, що накладаються, а в інтерференційних мінімумах – менша їх суми. Тобто, інтерференція хвиль призводить до перерозподілу енергії коливань між сусідніми областями середовища. Проте, в середньому для великої області простору енергія результуючої хвилі дорівнює сумі енергії хвиль, які інтерферують, як і повинно бути згідно з законом збереження та перетворення енергії.

Розглянемо окремий випадок інтерференції – виникнення стоячих хвиль. Стоячі хвилі виникають внаслідок накладання двох плоских хвиль з однаковими амплітудами і частотами, що поширюються назустріч одна одній. Поперечна стояча хвиля може утворитись, наприклад, в пружній нитці, один з кінців якої закріплений, а іншому надається коливальний рух.

При накладанні двох зустрічних когерентних плоских хвиль

,

,

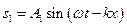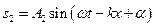де – різниця фаз хвиль в точці 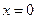, утворюється плоска стояча хвиля, що описується рівнянням:

.

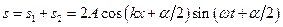Амплітуда 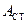стоячої хвилі є періодичною функцією координати:

.

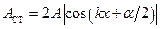Точки, в яких амплітуда стоячої хвилі 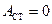, називаються вузлами стоячої хвилі, а точки, в яких амплітуда 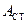максимальна і дорівнює 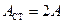, називаються пучностями стоячої хвилі. Положення вузлів і пучностей визначаються співвідношеннями:

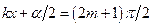(вузли),

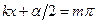(пучності),

де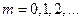

Відстані між сусідніми вузлами і між сусідніми пучностями однакові та дорівнюють половині довжини 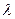біжучих хвиль. Таку величину називають довжиною стоячої хвилі: 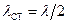. Відстань між сусідніми вузлом та пучністю стоячої хвилі становить 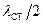. Відзначимо, що пружні механічні хвилі, які розглядались в попередніх розділах, також називаються біжучими, що підкреслює відмінність їхніх властивостей від стоячих хвиль. Зокрема, в біжучій хвилі фаза коливань залежить від координати розглядуваної точки, а у стоячій хвилі всі точки між двома вузлами коливаються з різними амплітудами, проте з однаковими фазами (синфазно), оскільки аргумент синуса в рівнянні стоячої хвилі не залежить від координати . При переході через вузол фаза коливань змінюється на 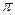, оскільки 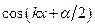при цьому змінює знак на протилежний.

На рис.10.3 наведено характер руху різних точок середовища натягненої пружної нитки довжиною l при встановленні в неї поперечної стоячої хвилі. Один з кінців нитки (ліворуч) коливають за гармонічним законом, а інший закріплено нерухомо. Стояча хвиля виникає при накладанні хвиль, які поширюються від джерела хвиль (вільного кінця нитки) до місця закріплення, і хвиль, що відбиваються від нього. При цьому слід врахувати, що при відбиванні хвилі від місця закріплення її фаза змінюється на 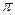, і у місці закріплення нитки виникає вузол стоячої хвилі. В точці О ( 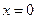) різниця фаз зустрічних хвиль 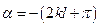. Кружками на рис.10.3 зображено вузли стоячої хвилі, а момент часу 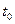обраний таким чином, що .

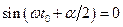В стоячій хвилі швидкість коливального руху частинок середовища

,

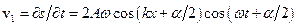а відносна деформація середовища

.

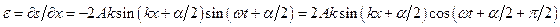Отже, на відміну від біжучої хвилі, у стоячій хвилі відносна деформація 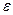середовища випереджає 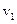на 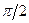. В моменти часу, коли швидкість коливального руху 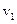набуває максимальної величини, 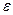стає рівним нулеві і навпаки. Крім того, величини 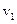і 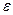залежать від координати по-різному: в пучностях стоячої хвилі знаходяться пучності швидкості частинок і вузли деформації середовища, а в вузлах стоячої хвилі – пучності деформації і вузли швидкості.

В пружній стоячій хвилі енергія періодично перетворюється з потенційної, яка локалізована головним чином поблизу пучностей деформації, в кінетичну, яка локалізована поблизу пучностей швидкості, і в зворотному напрямку. Тому енергія періодично мігрує від вузлів стоячої хвилі до її пучностей і навпаки. Проте, в самих вузлах і пучностях середня величина густини потоку енергії дорівнює нулеві. Середня за період величина густини потоку енергії дорівнює нулеві також в будь-якій точці стоячої хвилі, оскільки дві біжучі хвилі, що утворюють стоячу, переносять за період рівні величини енергії в протилежних напрямках. Така обставина і зумовила назву – стояча хвиля, що підкреслює відсутність переносу енергії в просторі.