Енергія пружних хвиль
Пружне середовище, в якому розповсюджуються механічні хвилі, характеризується кінетичною енергією коливного руху та потенційною енергію, зумовленою деформацією середовища. Якщо 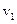 – швидкість частинок середовища, то об’ємна густина кінетичної енергії середовища:
– швидкість частинок середовища, то об’ємна густина кінетичної енергії середовища:
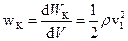 ,
,
де 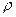 – густина середовища,
– густина середовища, 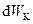 – кінетична енергія всіх частинок в малому об’ємі
– кінетична енергія всіх частинок в малому об’ємі 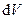 середовища (припускається, що в межах даного об’єму швидкість частинок однакова).
середовища (припускається, що в межах даного об’єму швидкість частинок однакова).
Об’ємна густина потенційної енергії пружно деформованого середовища
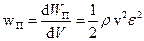 ,
,
де  – потенційна енергія однорідно деформованого невеликого об’єму середовища
– потенційна енергія однорідно деформованого невеликого об’єму середовища 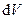 ,
, 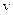 – фазова швидкість розповсюдження хвилі в середовищі,
– фазова швидкість розповсюдження хвилі в середовищі, 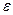 – відносна деформація.
– відносна деформація.
Під об’ємною густиною енергії пружних хвиль розуміють об’ємну густину  механічної енергії середовища, зумовлену поширенням цих хвиль:
механічної енергії середовища, зумовлену поширенням цих хвиль:
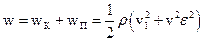 .
.
Якщо в середовищі поширюється плоска хвиля, то 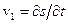 , де
, де 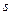 – зміщення частинок, і
– зміщення частинок, і 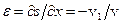 , тобто
, тобто  і
і
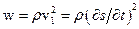 .
.
Для кожної точки середовища, яка залучена до коливного процесу, 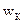 і
і 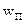 є однаковими функціями часу. Відповідно, і
є однаковими функціями часу. Відповідно, і  змінюється з часом. Така закономірність справедлива для будь-яких хвиль, що поширюються в пружному середовищі, незалежно від форми їх хвильових поверхонь та типу деформації середовища. Вона випливає з закону збереження енергії стосовно процесу поширення коливань в пружному середовищі. Для залучення в коливний процес все більш віддалених від джерела областей середовища необхідно втрачати енергію. Ця енергія надходить до середовища від джерела хвиль. Отже, поширення пружних хвиль нерозривно пов’язане з передачею енергії від одних областей середовища до інших. Саме тому об’ємна густина енергії пружних хвиль залежить від координати
змінюється з часом. Така закономірність справедлива для будь-яких хвиль, що поширюються в пружному середовищі, незалежно від форми їх хвильових поверхонь та типу деформації середовища. Вона випливає з закону збереження енергії стосовно процесу поширення коливань в пружному середовищі. Для залучення в коливний процес все більш віддалених від джерела областей середовища необхідно втрачати енергію. Ця енергія надходить до середовища від джерела хвиль. Отже, поширення пружних хвиль нерозривно пов’язане з передачею енергії від одних областей середовища до інших. Саме тому об’ємна густина енергії пружних хвиль залежить від координати  та часу
та часу 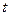 . Для плоскої монохроматичної хвилі така залежність за відсутності поглинання має вигляд:
. Для плоскої монохроматичної хвилі така залежність за відсутності поглинання має вигляд:
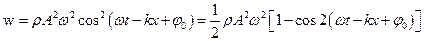 ,
,
де 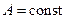 – амплітуда хвилі. У випадку сферичної хвилі за відсутності поглинання:
– амплітуда хвилі. У випадку сферичної хвилі за відсутності поглинання:
 ,
,
де 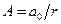 – амплітуда хвилі.
– амплітуда хвилі.
Середня за період величина об’ємної густини енергії
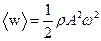 .
.
Швидкість переносу енергії хвилею дорівнює швидкості переміщення в просторі поверхні, яка відповідає максимальній величині густини об’ємної енергії хвилі. Для монохроматичних хвиль ця швидкість дорівнює фазовій швидкості 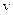 .
.
 Потоком енергії
Потоком енергії 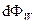 крізь невелику площадку
крізь невелику площадку 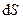 називається відношення енергії
називається відношення енергії  , яка переноситься через цю площадку
, яка переноситься через цю площадку 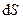 за невеликий проміжок часу, до його величини
за невеликий проміжок часу, до його величини 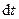 :
:
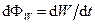 .
.
Якщо 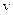 – швидкість переносу енергії плоскою хвилею (рис.10.1), то
– швидкість переносу енергії плоскою хвилею (рис.10.1), то
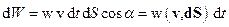 ,
,
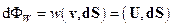 ,
,
де  – об’ємна густина енергії хвилі,
– об’ємна густина енергії хвилі, 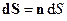 – вектор площадки
– вектор площадки 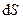 ,
, 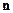 – одиничний вектор нормалі до площадки,
– одиничний вектор нормалі до площадки,  – кут між векторами
– кут між векторами 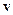 і
і  . Тут введено вектор
. Тут введено вектор
 ,
,
який спрямований в напрямку переносу енергії хвилею і називається вектором Умова (вектор густини потоку енергії хвилі). За модулем вектор Умова дорівнює відношенню потоку енергії 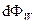 крізь невелику площадку
крізь невелику площадку 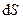 до площі
до площі 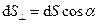 проекції цієї площадки на площину, яка перпендикулярна до напрямку переносу енергії:
проекції цієї площадки на площину, яка перпендикулярна до напрямку переносу енергії:  .
.
Інтенсивністю хвилі 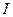 називається модуль середнього значення вектора Умова. Інтенсивність хвилі чисельно дорівнює енергії, яка переноситься хвилею за одиницю часу через одиницю площі поверхні, що перпендикулярна до напрямку поширення хвилі. Інтенсивність монохроматичної хвилі пропорційна квадрату її амплітуди. Зокрема, для плоскої та сферичної хвиль:
називається модуль середнього значення вектора Умова. Інтенсивність хвилі чисельно дорівнює енергії, яка переноситься хвилею за одиницю часу через одиницю площі поверхні, що перпендикулярна до напрямку поширення хвилі. Інтенсивність монохроматичної хвилі пропорційна квадрату її амплітуди. Зокрема, для плоскої та сферичної хвиль:
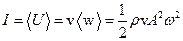 .
.
Якщо сферична хвиля поширюється в поглинальному середовищі, то за одиницю часу через будь-яку сферичну поверхню з радіусом 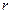 , центр якої збігається з джерелом хвилі, передається одна і та сама кількість енергії, яка дорівнює енергії, що витрачається джерелом:
, центр якої збігається з джерелом хвилі, передається одна і та сама кількість енергії, яка дорівнює енергії, що витрачається джерелом: 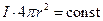 . Таким чином, інтенсивність і амплітуда сферичної хвилі зменшуються при віддаленні від центру хвилі за законами:
. Таким чином, інтенсивність і амплітуда сферичної хвилі зменшуються при віддаленні від центру хвилі за законами:
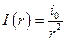 і
і  ,
,
де 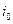 і
і 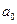 – інтенсивність та амплітуда хвилі на відстані 1 м від центра хвилі. Аналогічно можна показати, що в непоглинальному середовищі амплітуда А плоскої монохроматичної хвилі не залежить від координат.
– інтенсивність та амплітуда хвилі на відстані 1 м від центра хвилі. Аналогічно можна показати, що в непоглинальному середовищі амплітуда А плоскої монохроматичної хвилі не залежить від координат.
Перетворення енергії хвиль в інші види енергії, яке відбувається при поширенні хвиль в середовищі, зумовлює їх поглинання. В однорідному середовищі поглинання пружних хвиль відбувається в основному завдяки процесам внутрішнього тертя та теплопровідності. Амплітуда 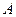 і інтенсивність
і інтенсивність 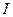 плоскої хвилі, яка поширюється в поглинальному середовищі вздовж додатного напрямку осі ОХ, змінюється за експоненційним законом:
плоскої хвилі, яка поширюється в поглинальному середовищі вздовж додатного напрямку осі ОХ, змінюється за експоненційним законом:
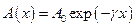 і
і 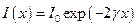 ,
,
де 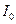 і
і 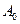 – відповідно інтенсивність і амплітуда хвилі в точці
– відповідно інтенсивність і амплітуда хвилі в точці 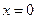 ,
, 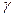 – лінійний коефіцієнт поглинання пружних хвиль.
– лінійний коефіцієнт поглинання пружних хвиль.
Дата добавления: 2015-04-07; просмотров: 2550;
