Аналогія величин і рівнянь поступального і обертального руху. Кінетична енергія обертання тіла
| Поступальний рух | Обертальний рух |
| S - шлях | φ – кут повороту |
| aτ –дотичне прискорення | ε – кутове прискорення |
| m - маса | J – момент інерції |
| F - сила | М – момент |
| P=mV - імпульс | L=Jω – момент імпульсу |
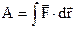 - робота - робота
| 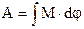 - робота - робота
|
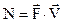 - потужність - потужність
| 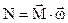 - потужність - потужність
|
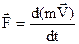 - 2-й з-н Ньютона - 2-й з-н Ньютона
| 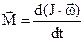 - осн. рівн-ня дин. оберт. руху. - осн. рівн-ня дин. оберт. руху.
|
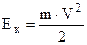 - кінетична енергія поступального руху - кінетична енергія поступального руху
| 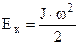 - кінетична енергія обертання тіла - кінетична енергія обертання тіла
|
Доведемо останню формулу. Кінетична енергія ∆Екі елементу тіла ∆mi дорівнює 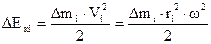 . Ми врахували зв’язок лінійної і кутової швидкостей
. Ми врахували зв’язок лінійної і кутової швидкостей 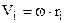 . Кінетичну енергію обертання всього тіла знайдемо як суму кінетичних енергій усіх його елементів, врахувавши (4.40), тобто
. Кінетичну енергію обертання всього тіла знайдемо як суму кінетичних енергій усіх його елементів, врахувавши (4.40), тобто 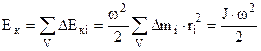 . (4.43)
. (4.43)
Якщо тіло не тільки обертається, а ще і його центр маси рухається поступально з швидкістю V, наприклад, котиться колесо, то кінетична енергія дорівнює сумі поступальної і обертальної складових
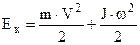 . (4.44)
. (4.44)
Дата добавления: 2015-06-17; просмотров: 1938;
