Amp; 7.2. Задачі, що приводять до диференціальних рівнянь.
Розглянемо задачі на складання диференціальних рівнянь.
Задача 1. Знайти закон руху тіла по осі ОХ, якщо воно почало рухатися з точки 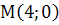 із швидкістю
із швидкістю 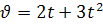 .
.
Розв’язання.
При прямолінійному русі швидкість є похідна від шляху за часом :
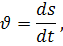
Маємо диференціальне рівняння :
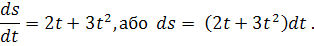
Проінтегрувавши, одержимо загальний розв’язок диференціального рівняння :
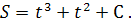
Використовуючи початкові умови при 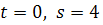 , знайдемо сталу інтегрування С :
, знайдемо сталу інтегрування С :
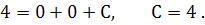
Підставимо значення 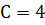 в загальний розв’язок, дістанемо частинний розв’язок; тобто закон руху тіла :
в загальний розв’язок, дістанемо частинний розв’язок; тобто закон руху тіла :
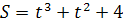 .
.
Задача 2. Скласти рівняння кривої, яка проходить через точку 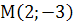 і має дотичну з кутовим коефіцієнтом
і має дотичну з кутовим коефіцієнтом 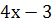 .
.
Розв’язання.
Із геометричного змісту похідної, маємо диференціальне рівняння :
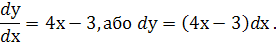
Проінтегрувавши, дістанемо загальний розв’язок диференціального рівняння : 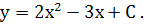
Використовуючи початкові умови 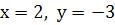 , знаходимо
, знаходимо 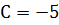 .
.
Отже, шукане рівняння кривої має вигляд: 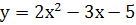 .
.
Дата добавления: 2015-06-27; просмотров: 4079;
