Лінійні диференціальні рівняння першого порядку.
Рівняння вигляду
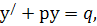
де 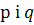 - функції від х або сталі величини, називається лінійним диференціальним рівнянням першого порядку.
- функції від х або сталі величини, називається лінійним диференціальним рівнянням першого порядку.
Це рівняння зводиться до рівняння з відокремлюваними змінними за допомогою підстановки 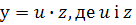 - нові функції від х.
- нові функції від х.
Приклад3. Знайти частинний розв’язок рівняння 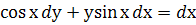 , якщо
, якщо 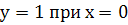 .
.
Розв’язання.
Поділивши всі члени рівняння на 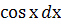 , дістанемо рівняння
, дістанемо рівняння
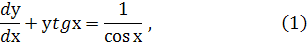
яке є лінійним. Припустимо, що 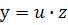 , тоді
, тоді 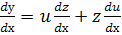 . Підставивши вирази для у і
. Підставивши вирази для у і 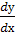 в рівняння
в рівняння 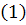 , маємо
, маємо
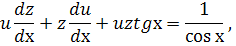
або
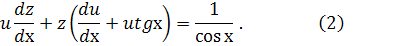
Для відшукання 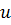 дістанемо рівняння
дістанемо рівняння
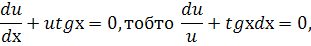
звідки
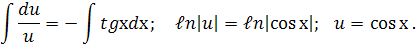
Підставивши вираз для 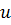 в рівняння
в рівняння 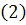 , маємо, маємо
, маємо, маємо
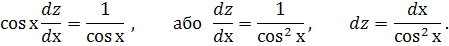
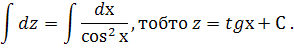
Отже, загальний розв’язок рівняння записується так :
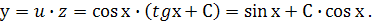
Використовуючи початкові умови 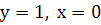 , маємо
, маємо

Частинний розв’язок має вигляд
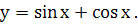
Дата добавления: 2015-06-27; просмотров: 1839;
