Однорідні диференціальні рівняння першого порядку.

Однорідною функцією змінних х і у називається функція, всі члени якої мають однаковий степінь.

Наприклад, 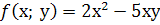- однорідна функція другого степеня.

Рівняння вигляду

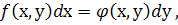
де 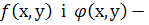однорідні функції одного й того самого степеня, називається однорідним.

Однорідне рівняння за допомого підстановки 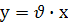зводиться до рівняння з відокремлюваними змінними.

Приклад 2. Знайти загальний розв’язок рівняння

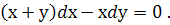
Розв’язання.

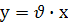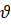Дане рівняння є однорідним рівнянням першого степеня відносно змінних х і у. Припустимо, що , де - нова функція від х. Знайдемо диференціал добутку :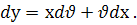

Підставивши вирази у і 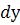в дане рівняння, дістанемо

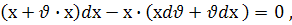
звідки, зробивши спрощення, маємо :

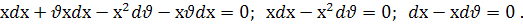
Дістали рівняння з відокремлюваними змінними.

Відокремивши змінні та проінтегрувавши, знаходимо :

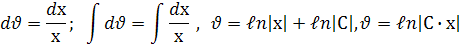
Замінивши в цьому виразі 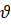на , дістанемо 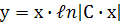. Це і є загальний розв’язок рівняння.