Amp; 1.2. Системи лінійних рівнянь з трьома змінними. Визначник третього порядку та його властивості. Мінор та алгебраїчне доповнення. Обчислення визначника третього порядку.
Розглянемо систему лінійних рівнянь з трьома змінними :

Таблиця 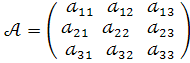 називається квадратною
називається квадратною
матрицею третього порядку.
Кожній квадратній матриці ставиться у відповідність числова характеристика, яка називається визначником третього порядку та позначається 
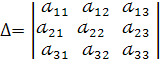
Мінором 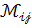 елемента
елемента 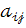 визначника третього порядку називається визначник другого порядку, який одержується з
визначника третього порядку називається визначник другого порядку, який одержується з  внаслідок викреслювання
внаслідок викреслювання 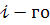 рядка та
рядка та 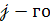 стовпця.
стовпця.
Наприклад : 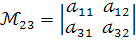
Алгебраїчним доповненням 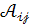 елемента
елемента 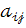 визначника
визначника  називається його мінор, помножений на
називається його мінор, помножений на 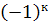 , де к – сума номерів рядка і стовпця, які містять даний елемент.
, де к – сума номерів рядка і стовпця, які містять даний елемент.
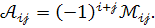
Наприклад : 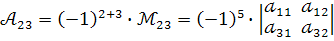
Визначник  є сума добутків елемента рядка (стовпця) на відповідні алгебраїчні доповнення, тобто :
є сума добутків елемента рядка (стовпця) на відповідні алгебраїчні доповнення, тобто :
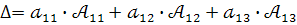
Цю рівність називають розкладом визначника за елементами першого рядка.
Таким чином, визначник третього порядку обчислюють за формулою :
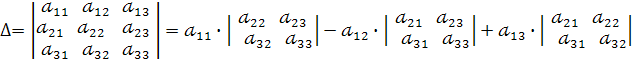
Приклад 2. Обчислити
2 1</m:t></m:r></m:e></m:eqArr></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 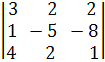
Розв’язання.
Розкладемо визначник за елементами першого рядка :
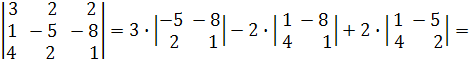
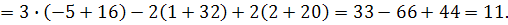
Дата добавления: 2015-06-27; просмотров: 3477;
