Обернена матриця

Квадратна матриця 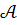називається невиродженою, якщо її визначник 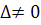. Якщо 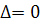, то матриця 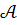називається виродженою.

Всяка невироджена матриця 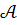має обернену матрицю 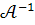таку, що

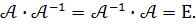
Обернена матриця для невиродженої матриці 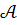визначається за формулою :

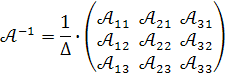
Приклад 7.Знайти 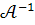, якщо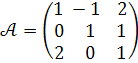

Розв’язання.

Спочатку знаходимо визначник матриці :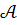

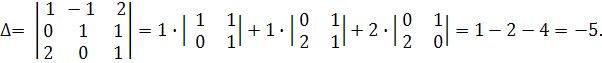
Отже, матриця невироджена, і існує .

Обчислюємо алгебраїчні доповнення :

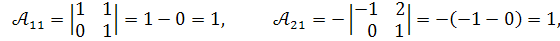
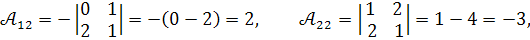
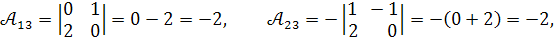
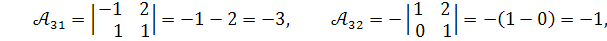
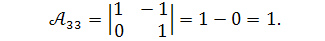
Обернена матриця дорівнює :

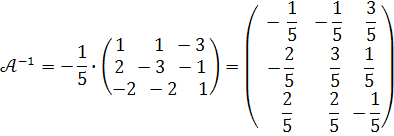
Для перевірки правильності розв’язку задачі знаходимо добуток 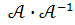. Якщо 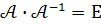, то обернена матриця знайдена правильно.

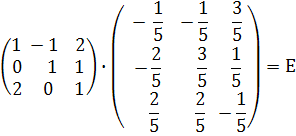
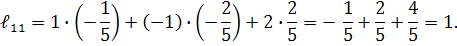
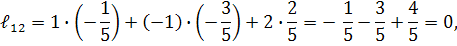
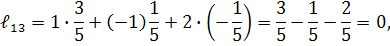
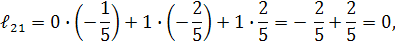
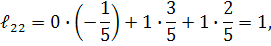
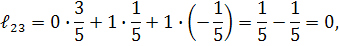
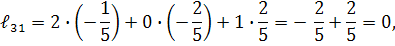
s w:val="28"/></w:rPr><m:t>=0,</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">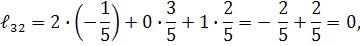

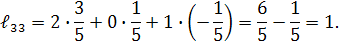
Таким чином, ми одержали одиничну матрицю

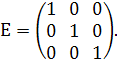
А це значить, що обернена матриця 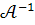знайдена правильно.