Властивості визначників
1. Визначник не зміниться, якщо в ньому рядки замінити стовпцями.
2. При перестановці місцями двох рядків (стовпців) визначник змінює знак на протилежний.
3. Якщо визначник має два однакові рядки (стовпці), то він дорівнює нулю.
4. Якщо всі елементи рядка (стовпця) мають спільний множник, то його можна винести за знак визначника.
5. Якщо елементи якого-небудь рядка (стовпця) пропорційні відповідним елементам другого рядка (стовпця), то такий визначник дорівнює нулю.
6. Якщо кожен елемент рядка (стовпця) визначника є сумою двох доданків, то його можна записати як суму двох визначників.
7. Значення визначника не зміниться, якщо до елементів рядка (стовпця) додати відповідні елементи другого рядка (стовпця) цього визначника, домножені на число 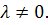
Розглянемо на прикладі, як користуватися цими властивостями.
Приклад 3. Обчислити визначник
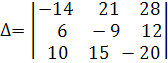
Розв’язання.
Винесемо за знак визначника спільні множники елементів кожного рядка:
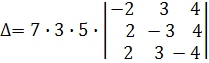 ,
,
а потім третій рядок додамо до першого і другого :
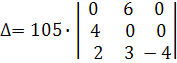
Розкладемо визначник по елементам першого рядка, одержимо
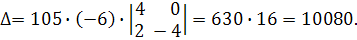
& 1.3. Матриці. Дії над матрицями. Обернена матриця.
Квадратна матриця
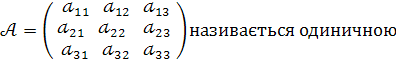
та позначається літерою Е :
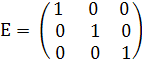
Матриця – рядок – це матриця виду
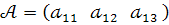
Матриця – стовпець – це матриця виду
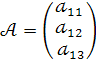
Дата добавления: 2015-06-27; просмотров: 1558;
