Розв’язування систем лінійних рівнянь матричним способом.

Розглянемо систему трьох лінійних рівнянь відносно трьох невідомих

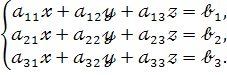
Її можна записати у матричному вигляді. Для цього позначимо

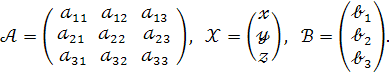
Систему можна записати так :

Матричним способом можна розв’язати систему тільки тоді, коли
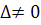, тобто існує .

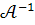Помножимо систему на 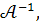одержимо :

Враховауючи властивість добутку, маємо :

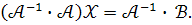
За визначенням оберененої матриці, маємо

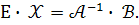
Оскільки 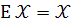, то одержуємо

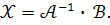
Це розв’язок систем у матричній формі.

Приклад 10. Розв’язати систему рівнянь матричним способом :

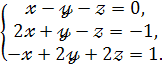
Розв’язання.

Запишемо систему у матричній формі

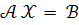, де

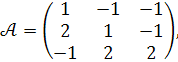
Перевіримо, чи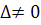

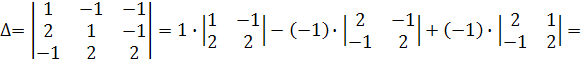
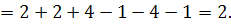
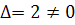. Отже існує обернена матриця 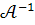, яку знаходимо за формулою :

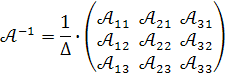
Обчислимо алгебраїчні доповнення :

.

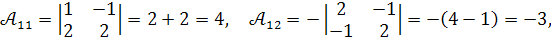
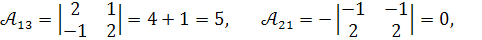
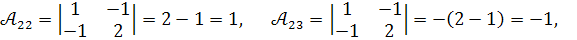
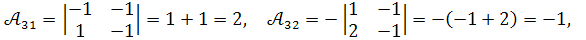
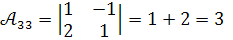Отже

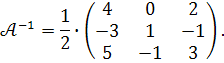
Тоді

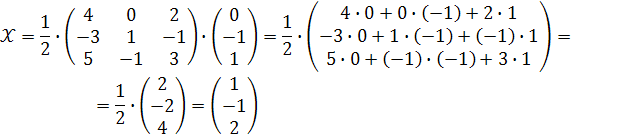
Відповідь :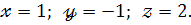

Питання для самоконтролю.

1. Як обчислюється визначник другого порядку ?

2. Що таке мінор та алгебраїчне доповнення?

3. Як обчислюється визначник третього порядку?

4. Які властивості визначників?

5. Які дії виконуються над матрицями?

6. За якою формулою знаходиться обернена матриця?

7. Як розв’язується система лінійних рівнянь методом Гауса?

8. Як розв’язується система лінійних рівнянь за формулами Крамера?

9. Як розв’язується система лінійних рівнянь матричним способом?