amp; 7.5. Лінійні однорідні рівняння другого порядку зі сталими коефіцієнтами. Загальний та частинний розв’язки.
Лінійним однорідним диференціальним рівнянням другого порядку зі сталими коефіцієнтами називається рівняння виду:
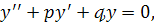 де
де 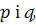 - сталі величини.
- сталі величини.
Щоб знайти загальний розв’язок рівняння, потрібно скласти характеристичне рівняння 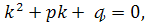 яке дістаємо з рівняння заміною
яке дістаємо з рівняння заміною 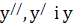 на відповідні степені к, причому сама функція у замінюється одиницею.
на відповідні степені к, причому сама функція у замінюється одиницею.
Загальний розв’язок будується залежно від коренів k1 і k2 характеристичного рівняння.
Випадок 1 . Корені k1 і k2 – дійсні і різні.
Загальний розв’язок рівняння має вигляд:
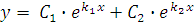
Випадок 2 . Корені k1 і k2 – дійсні і рівні. k1 = k2 = k .
Загальний розв’язок рівняння має вигляд:
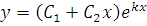
Випадок 3 . Корені k1 і k2 – комплексні спряжені: k1 = 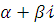 ; k2 =
; k2 = 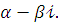
Загальний розв’язок рівняння має вигляд:
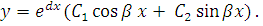
Приклад 4. Розв’язати рівняння :
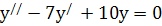
Розв’язання.
Складаємо характеристичне рівняння:
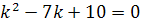 ,
, 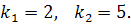
Корені характеристичного рівняння дійсні і різні, то загальний розв’язок диференціального рівняння запишеться так:
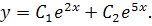
Приклад 5. Розв’язати рівняння 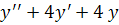 = 0.
= 0.
Розв’язання
Складаємо характеристичне рівняння:
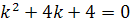 ,
, 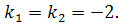
Корені характеристичного рівняння дійсні і рівні, отже загальний розв’язок диференціального рівняння запишеться так:
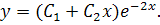
Приклад 6. Розв’язати рівняння 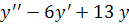 = 0.
= 0.
Розв’язання
Характеристичне рівняння 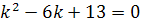 має комплексні корені
має комплексні корені
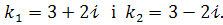
Загальний розв’язок диференціального рівняння запишеться так:
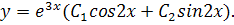
Приклад 7. Знайти частинний розв’язок рівняння
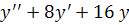 = 0 , якщо
= 0 , якщо 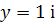
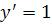 при х = 0.
при х = 0.
Розв’язання
Характеристичне рівняння 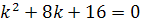 , має рівні дійсні корені
, має рівні дійсні корені 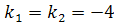 , то загальний роз’вязок диференціального рівняння запишеться так:
, то загальний роз’вязок диференціального рівняння запишеться так:
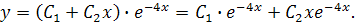
Диференціюючи загальний розв’язок, маємо
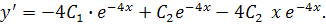
Підставимо початкові дані у вирази для 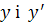 , дістанемо систему рівнянь:
, дістанемо систему рівнянь:
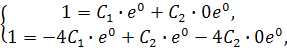 або
або 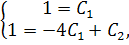
звідки C1 = 1 і C2 = 5.
Отже, шуканий частинний розв'язок має вигляд
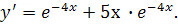
Дата добавления: 2015-06-27; просмотров: 8977;
